Question

【题目】已知集合A={x||2x﹣1|≤3}，集合B={x|x2+（4﹣a）x﹣4a＞0}，若A∩B=A，求实数a的取值范围．

Answer 1

【答案】解：由题意：集合A={x||2x﹣1|≤3}={x|﹣1≤x≤2}
集合B={x|x2+（4﹣a）x﹣4a＞0}={x|（x+4）（x﹣a）＞0}，
∵A∩B=A
∴AB．
解法一：
令f（x）=x2+（4﹣a）x﹣4a＞0，
∵﹣1≤x≤2，
根据一元二次方程的根的分布：
可得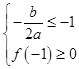： 或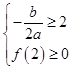
解：a≤﹣1
故得实数a的取值范围是：（﹣∞，﹣1]．
解法二，讨论思想：
当a=﹣4时，B={x∈R|x≠﹣4}，满足AB．
当a＞﹣4时，B={x|x＞a或x＜﹣4}，
要使AB成立，则：a≤﹣1．
当a＜﹣4时，B={x|x＜a或x＞﹣4}，满足AB．
故得实数a的取值范围是：（﹣∞，﹣1]
【解析】确定集合A的元素范围，根据A∩B=A，建立条件关系即可求实数a的取值范围．