题目内容
【题目】设全集U=R．
（1）解关于x的不等式|x﹣1|+a﹣1＞0（a∈R）；
（2）记A为（1）中不等式的解集，B为不等式组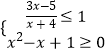 
的整数解集，若（UA）∩B恰有三个元素，求a的取值范围．
【答案】
（1）解：由|x﹣1|+a﹣1＞0 得|x﹣1|＞1﹣a，
当a＞1时，解集是R；
当a≤1时，解集是{x|x＜a，或 x＞2﹣a}
（2）解：解不等式组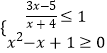 
，得：﹣4＜x≤ 
，
故B={﹣3，﹣2，﹣1，0，1，2，3，4}，
当a＞1时，CUA=，不满足条件．
当a≤1时，CUA={x|a≤x≤2﹣a}，∴2﹣a≥1，
若（UA）∩B恰有三个元素，
则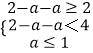 
，解得：﹣1＜a≤0
【解析】（1）通过讨论a的范围，求出不等式的解集即可；（2）解不等式组，求出集合B，通过讨论a的范围，求出∪A，结合题意得到关于a的不等式，解出即可．
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识，掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．
练习册系列答案
相关题目
【题目】从一批土鸡蛋中，随机抽取n个得到一个样本，其重量（单位：克）的频数分布表如表：
分组（重量） | [80，85） | [85，90） | [90，95） | [95，100] |
频数（个） | 10 | 50 | m | 15 |
已知从n个土鸡蛋中随机抽取一个，抽到重量在在[90，95）的土鸡蛋的根底为 
（1）求出n，m的值及该样本的众数；
（2）用分层抽样的方法从重量在[80，85）和[95，100）的土鸡蛋中共抽取5个，再从这5个土鸡蛋中任取2 个，其重量分别是g1 ， g2 ， 求|g1﹣g2|≥10概率．
