题目内容
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆方程;
(2)斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且与椭圆交于
,且与椭圆交于![]() 两点,
两点, ![]() 为直线
为直线![]() 上的一点,若△
上的一点,若△![]() 为等边三角形,求直线
为等边三角形,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.
【解析】试题分析:本题主要考查椭圆的标准方程以及几何性质、直线与椭圆相交问题、韦达定理、两点间距离公式、直线的方程等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用椭圆的标准方程中a,b,c的关系,焦点坐标,离心率列出方程组,解出a和b,从而得到椭圆的标准方程;第二问,点斜式设出直线方程,由于直线与椭圆交于A,B,则直线与椭圆方程联立消参得到关于x的方程,设出A,B点坐标,利用韦达定理,得到![]() ,
, ![]() ,再结合两点间距离公式求出
,再结合两点间距离公式求出![]() 的长,利用中点坐标公式得出AB中点M的坐标,从而求出|MP|的长,利用
的长,利用中点坐标公式得出AB中点M的坐标,从而求出|MP|的长,利用![]() 为正三角形,则
为正三角形,则![]() ,列出等式求出k的值,从而得到直线的方程.
,列出等式求出k的值,从而得到直线的方程.
(1)依题意有![]() ,
, ![]() .
.
可得![]() ,
, ![]() .
.
故椭圆方程为![]() . 5分
. 5分
(2)直线![]() 的方程为
的方程为![]() .
.
联立方程组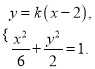
消去![]() 并整理得
并整理得![]() .
.
设![]() ,
, ![]() .
.
故![]() ,
, ![]() .
.
则![]()
![]() .
.
设![]() 的中点为
的中点为![]() .
.
可得![]() ,
, ![]() .
.
直线![]() 的斜率为
的斜率为![]() ,又
,又![]() ,
,
所以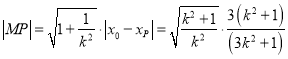 .
.
当△![]() 为正三角形时,
为正三角形时,![]() ,
,
可得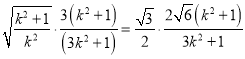 ,
,
解得![]() .
.
即直线![]() 的方程为
的方程为![]() ,或
,或![]() . 13分
. 13分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

