题目内容
【题目】如果设奇函数f（x）在（0，+∞）上为增函数，且f（2）=0，则不等式 
＜0的解集为（ ）
A.（﹣2，0）∪（2，+∞）
B.（﹣∞，﹣2）∪（0，2）
C.（﹣∞，﹣2）∪（2，+∞）
D.（﹣2，0）∪（0，2）
【答案】D
【解析】解：由函数f（x）为奇函数，可得不等式即 
，即 x和f（x）异号，
故有 
，或 
．
再由f（2）=0，可得f（﹣2）=0，
由函数f（x）在（0，+∞）上为增函数，可得函数f（x）在（﹣∞，0）上也为增函数，
结合函数f（x）的单调性示意图可得，﹣2＜x＜0，或 0＜x＜2，
故选 D．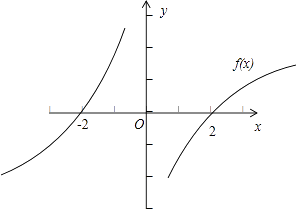
【考点精析】通过灵活运用奇偶性与单调性的综合，掌握奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性即可以解答此题．
练习册系列答案
相关题目
【题目】从一批土鸡蛋中，随机抽取n个得到一个样本，其重量（单位：克）的频数分布表如表：
分组（重量） | [80，85） | [85，90） | [90，95） | [95，100] |
频数（个） | 10 | 50 | m | 15 |
已知从n个土鸡蛋中随机抽取一个，抽到重量在在[90，95）的土鸡蛋的根底为 
（1）求出n，m的值及该样本的众数；
（2）用分层抽样的方法从重量在[80，85）和[95，100）的土鸡蛋中共抽取5个，再从这5个土鸡蛋中任取2 个，其重量分别是g1 ， g2 ， 求|g1﹣g2|≥10概率．
