题目内容
11.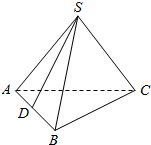 如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
分析 取AC中点E,连接DE、SE.在△ABC中利用中位线定理得DE∥BC,所以∠SDE(或其补角)即为异面直线SD与BC所成的角,设正四面体棱长为a,算出△SDE中各边之长,再利用余弦定理加以计算可得答案.
解答  解:取AC中点E,连接DE、SE,
解:取AC中点E,连接DE、SE,
∵△ABC中D,E分别为AB、AC的中点,∴DE∥BC,DE=$\frac{1}{2}$BC
因此,∠SDE(或其补角)即为异面直线SD与BC所成的角,
设正四面体棱长为a,由题意可得SD=SE=$\frac{\sqrt{3}}{2}$a,DE=$\frac{1}{2}$a,
∴在△SDE中,根据余弦定理得
cos∠SDE=$\frac{D{E}^{2}+S{D}^{2}-S{E}^{2}}{2DE×SD}$=$\frac{\frac{1}{4}{a}^{2}+\frac{3}{4}{a}^{2}-\frac{3}{4}{a}^{2}}{2×\frac{1}{2}a×\frac{\sqrt{3}}{2}a}$=$\frac{\sqrt{3}}{6}$
即异面直线AE和BD所成角的余弦值为 $\frac{\sqrt{3}}{6}$;
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题在正四面体中求异面直线所成角大小.着重考查了正四面体的性质、三角形的中位线定理和异面直线所成角的定义及其求法等知识,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
1.一几何体的三视图如图所示,则它的体积为( )
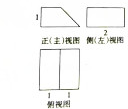

| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
19.设S是整数集Z的非空子集,如果?a,b∈Z,都有a2-b2∈S,则称S是一个好集,已知S是一个“好集”,下面命题为假命题的是( )
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
6.4位同学要完成100米的接力跑,要求每个人跑的路程不超过其他任一同学所跑路程的3倍,若某一同学所跑路程为x米,则x的取值范围为( )
| A. | 10≤x≤20 | B. | 10≤x≤30 | C. | 20≤x≤40 | D. | 10≤x≤50 |
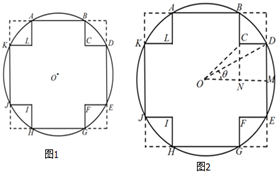 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心) 如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.
如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.