题目内容
1. 如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.
如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.(1)求:$\overrightarrow{DF}$.
(2)求∠BAC的余弦值.
分析 (1)根据向量的坐标公式进行计算即可求:$\overrightarrow{DF}$.
(2)利用数量积的应用即可求∠BAC的余弦值.
解答 解:(1)∵A(7,8),B(3,5),C(4,3),
∴$\overrightarrow{AB}$=(-4,-3),$\overrightarrow{AC}$=(-3,-5),
∵D是BC的中点,
∴$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=($-\frac{7}{2}$,-4),
∵M,N分别是AB,AC的中点,
∴F是AD的中点,
∴$\overrightarrow{DF}=-\overrightarrow{FD}=-\frac{1}{2}(-\frac{7}{2},-4)$=($\frac{7}{4}$,2).
(2)∵$\overrightarrow{AB}$=(-4,-3),$\overrightarrow{AC}$=(-3,-5),
∴cos∠BAC=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{-4×(-3)+(-3)×(-5)}{5×\sqrt{34}}$=$\frac{27\sqrt{34}}{170}$.
点评 本题主要考查平面向量的基本运算以及利用数量积求向量夹角问题,比较基础.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
11. 如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )
如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )
 如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )
如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,1.6 | B. | 84,1.6 | C. | 84,4.84 | D. | 85,4 |
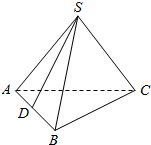 如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.
如图,在正四面体S-ABC(四个面都是等边三角形)中,点D是棱AB的中点,则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$.