题目内容
1．一几何体的三视图如图所示，则它的体积为（ ）
| A． | 2 | B． | 3 | C． | 6 | D． | 9 |
分析 由三视图可得：该几何体是四棱柱，利用体积公式即可得出．
解答 解：由三视图可得：该几何体是四棱柱，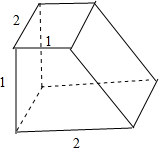
底面积=$\frac{1×（1+2）}{2}$=$\frac{3}{2}$，高为2，
∴V=$\frac{3}{2}×2$=3．
故选：B．
点评 本题考查了四棱柱的三视图及其体积计算公式，属于基础题．
练习册系列答案
相关题目
11．
如图过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”，则椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的“左特征点”M的坐标为（ ）
如图过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”，则椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的“左特征点”M的坐标为（ ）| A． | （-2，0） | B． | （-3，0） | C． | （-4，0） | D． | （-5，0） |
12．要得到y=cos2x的图象，可由函数y=cos（2x-$\frac{π}{3}$）的图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位长度 | B． | 向右平移$\frac{π}{3}$个单位长度 | ||
| C． | 向左平移$\frac{π}{6}$个单位长度 | D． | 向右平移$\frac{π}{6}$个单位长度 |
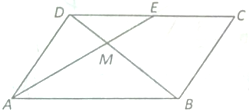
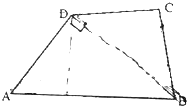在四边形ABCD中，AB=$\sqrt{3}$，BC=CD=DA=1，△ABD和△BCD的面积分别为m，n．
如图，在正四面体S-ABC（四个面都是等边三角形）中，点D是棱AB的中点，则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$．