题目内容
已知数列 ,满足
,满足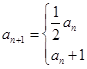
 ,
, ,若
,若 。
。
(1)求 ; (2)求证:
; (2)求证: 是等比数列; (3)若数列
是等比数列; (3)若数列 的前
的前 项和为
项和为 ,求
,求
(1) ; (2)详见解析;(3)
; (2)详见解析;(3) .
.
解析试题分析:(1)根据题中所给数列的递推关系 ,由已知
,由已知 推出
推出 ,再由所得
,再由所得 推出
推出 ,最后由
,最后由 求出
求出 的值;(2)要证明是
的值;(2)要证明是 等比数列,即可联想到等比数列的定义去证明
等比数列,即可联想到等比数列的定义去证明 常数,将由所给
常数,将由所给 代入到
代入到 ,化简得到这是一个常数,进而得到
,化简得到这是一个常数,进而得到 是一个等比数列; (3)由(2)中所求
是一个等比数列; (3)由(2)中所求 是一个等比数列,结合等比数列的通项公式中的
是一个等比数列,结合等比数列的通项公式中的 ,可求出
,可求出 的通项,进而得出
的通项,进而得出 的表达式,并由此求出所有奇数项的和
的表达式,并由此求出所有奇数项的和 ,又由
,又由 求出
求出 的表达式,并由此求出所有偶数项的和
的表达式,并由此求出所有偶数项的和 ,最后由
,最后由 求出
求出 的表达式.
的表达式.
试题解析:(1)
 ;
;
(2)证明: ,故数列
,故数列 是首项为
是首项为 ,公比为
,公比为 的等比数列;
的等比数列;
(3) ,即
,即 ,
, ,又
,又 ,
, .
.
考点:1.数列的通项;2.等比数列的定义;3.数列的求和

练习册系列答案
相关题目
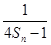 ,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由. 的前n项和为
的前n项和为
 ,
,
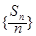 为等差数列;
为等差数列; 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn. ,数列
,数列 是首项为
是首项为 ,公比也为
,公比也为
 的前
的前 项和
项和 ;
; 为递增数列,且
为递增数列,且 ,
, .(Ⅰ)求
.(Ⅰ)求 ;
; ,不等式
,不等式 的解集为
的解集为 ,求所有
,求所有 的和.
的和. 的前
的前 项和为
项和为 ,且
,且 ,
, .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 .
. 中,
中,
 是等比数列,并求
是等比数列,并求 ;
; 满足
满足 ,数列
,数列 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围。
的取值范围。 }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.  求数列
求数列 的前
的前 项和
项和 .
. ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 ;数列
;数列 为公比大于
为公比大于 的等比数列,且
的等比数列,且 为方程
为方程 的两个不相等的实根.
的两个不相等的实根. 项,第
项,第 项,第
项,第 项,……,第
项,……,第 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列 ,求数列
,求数列 项和.
项和.