题目内容
已知 ,数列
,数列 是首项为
是首项为 ,公比也为
,公比也为 的等比数列,令
的等比数列,令
(Ⅰ)求数列 的前
的前 项和
项和 ;
;
(Ⅱ)当数列 中的每一项总小于它后面的项时,求
中的每一项总小于它后面的项时,求 的取值范围.
的取值范围.
(1) ;(2)
;(2)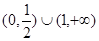 .
.
解析试题分析:本题考查数列的通项公式和数列求和问题,考查学生的计算能力和分析问题解决问题的能力,考查分类讨论思想和转化思想.第一问,利用等比数列的通项公式先写出数列 的通项公式,利用对数的性质得到
的通项公式,利用对数的性质得到 的通项公式,从而列出
的通项公式,从而列出 ,它符合错位相减法,利用错位相减法求和;第二问,有题意得
,它符合错位相减法,利用错位相减法求和;第二问,有题意得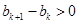 ,讨论
,讨论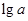 的正负,转化为恒成立问题,求出
的正负,转化为恒成立问题,求出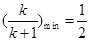 .
.
试题解析:(Ⅰ)由题意知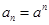 ,
,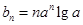 .
.
∴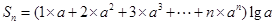 .
.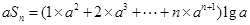 .
.
以上两式相减得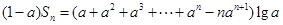
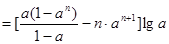 .
.
∵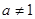 ,∴
,∴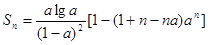 .
.
(Ⅱ)由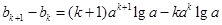
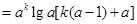 .
.
由题意知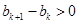 ,而
,而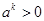 ,
,
∴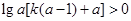 . ①
. ①
(1)若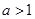 ,则
,则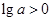 ,
,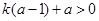 ,故
,故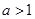 时,不等式①成立;
时,不等式①成立;
(2)若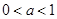 ,则
,则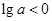 ,
,
不等式①成立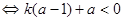
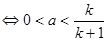 恒成立
恒成立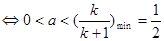 .
.
综合(1)、(2)得 的取值范围为
的取值范围为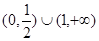 .
.
考点:1.等比数列的通项公式;2.等比数列的前n项和公式;3.错位相减法;4.恒成立问题.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
, ,
, .证明:数列
.证明:数列 是公比为
是公比为 的等比数列的充要条件是
的等比数列的充要条件是 .
. }的前n项和为
}的前n项和为 ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, .求不超过
.求不超过 的最大整数的值.
的最大整数的值. 的前n项和中,
的前n项和中, 最小,且
最小,且 ,前n项和
,前n项和 ,求n和公比q
,求n和公比q ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示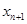 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前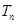 ,求
,求 ,满足
,满足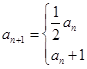
 ,
, ,若
,若 。
。 ; (2)求证:
; (2)求证: 是等比数列; (3)若数列
是等比数列; (3)若数列 项和为
项和为 ,求
,求
 的前
的前 项和是
项和是 ,且
,且 .
. ,求适合方程
,求适合方程 的正整数
的正整数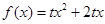
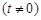
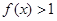 的解集;
的解集;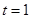 ,记
,记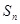 为数列
为数列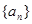 的前
的前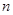 项和,且
项和,且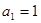 ,
,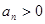
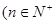 ),点
),点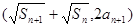 在函数
在函数 的图像上,求
的图像上,求