题目内容
已知等比数列 为递增数列,且
为递增数列,且 ,
, .(Ⅰ)求
.(Ⅰ)求 ;
;
(Ⅱ)令 ,不等式
,不等式 的解集为
的解集为 ,求所有
,求所有 的和.
的和.
(Ⅰ)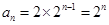 ;(Ⅱ)所有
;(Ⅱ)所有 的和
的和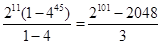 .
.
解析试题分析:(Ⅰ)设 的首项为
的首项为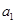 ,公比为
,公比为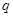 ,
,
依题意可建立其方程组,不难求得.
(Ⅱ)根据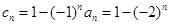 , 要注意分
, 要注意分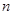 为偶数,
为偶数, 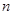 为奇数,加以讨论,明确
为奇数,加以讨论,明确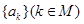 是首项为
是首项为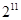 ,公比为
,公比为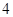 的等比数列,利用等比数列的求和公式,计算得到所有
的等比数列,利用等比数列的求和公式,计算得到所有 的和.
的和.
试题解析:(Ⅰ)设 的首项为
的首项为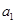 ,公比为
,公比为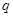 ,
,
所以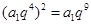 ,解得
,解得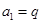 2分
2分
又因为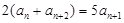 ,所以
,所以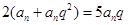
则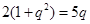 ,
,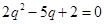 ,解得
,解得 (舍)或
(舍)或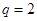 4分
4分
所以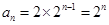 6分
6分
(Ⅱ)则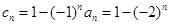 ,
,
当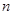 为偶数,
为偶数,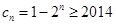 ,即
,即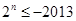 ,不成立 8分
,不成立 8分
当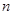 为奇数,
为奇数,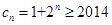 ,即
,即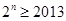 ,
,
因为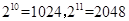 ,所以
,所以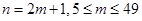 10分
10分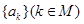 组成首项为
组成首项为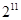 ,公比为
,公比为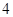 的等比数列,则所有
的等比数列,则所有 的和
的和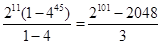 12分
12分
考点:等比数列的通项公式、求和公式

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
 的前n项和中,
的前n项和中, 最小,且
最小,且 ,前n项和
,前n项和 ,求n和公比q
,求n和公比q
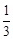 .
. ,满足
,满足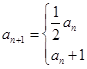
 ,
, ,若
,若 。
。 ; (2)求证:
; (2)求证: 是等比数列; (3)若数列
是等比数列; (3)若数列 项和为
项和为 ,求
,求
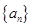 的前
的前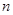 项和为
项和为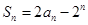 ,
,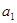 ,
,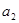 ;
;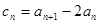 ,证明:数列
,证明:数列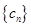 是等比数列;
是等比数列;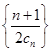 的前
的前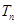 .
.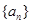 满足
满足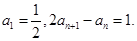
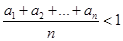 .
.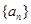 中,
中,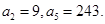
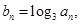 求数列{
求数列{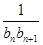 }的前
}的前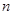 项和
项和