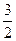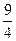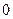题目内容
(本题满分12分)在直角坐标平面中,△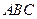 的两个顶点
的两个顶点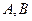 的坐标分别为
的坐标分别为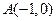 ,
,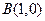 ,平面内两点
,平面内两点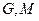 同时满足下列条件:①
同时满足下列条件:①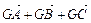 =0;②
=0;②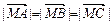 ;③
;③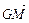 ∥
∥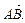 (1)求△
(1)求△ 的顶点
的顶点 的轨迹方程;(2)过点
的轨迹方程;(2)过点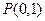 直线
直线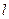 与(1)中轨迹交于不同的两点
与(1)中轨迹交于不同的两点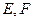 ,求△
,求△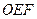 面积的最大值.
面积的最大值.
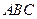 的两个顶点
的两个顶点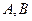 的坐标分别为
的坐标分别为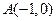 ,
,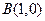 ,平面内两点
,平面内两点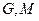 同时满足下列条件:①
同时满足下列条件:①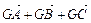 =0;②
=0;②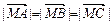 ;③
;③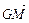 ∥
∥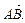 (1)求△
(1)求△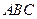 的顶点
的顶点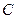 的轨迹方程;(2)过点
的轨迹方程;(2)过点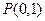 直线
直线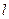 与(1)中轨迹交于不同的两点
与(1)中轨迹交于不同的两点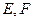 ,求△
,求△ 面积的最大值.
面积的最大值.(Ⅰ)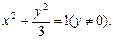 (Ⅱ)
(Ⅱ) 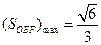
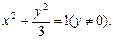 (Ⅱ)
(Ⅱ) 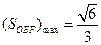
(1)设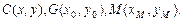 ∵
∵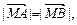
∴M点在线段AB的中垂线上.由已知A(-1,0),B(1,0),∴xM="0. "
∴(-1-x0,-y0)+(1-x0,-y0)+(x-x0,y-y0)=(0,0),∴x0=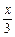 ,y0=
,y0=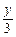 ,∴
,∴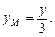 ∵
∵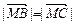 ,∴
,∴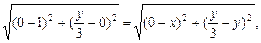
∴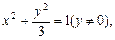 ∴顶点C的轨迹方程为
∴顶点C的轨迹方程为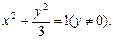 (4分)
(4分)
(2)设直线l方程为: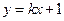 ,E(x1,y1),F(x2,y2),
,E(x1,y1),F(x2,y2),
由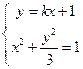 ,消去y得:
,消去y得: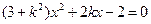 ①
①
∴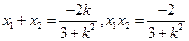 (6分)
(6分)
∴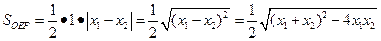 ,
,
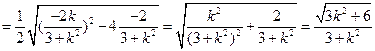
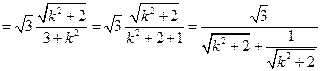 -----10分
-----10分
设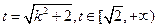 ,则
,则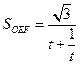 在
在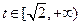 单调递减。
单调递减。
故当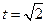 ,即
,即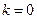 时,
时,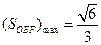 ----12分
----12分
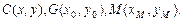 ∵
∵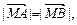
∴M点在线段AB的中垂线上.由已知A(-1,0),B(1,0),∴xM="0. "
∴(-1-x0,-y0)+(1-x0,-y0)+(x-x0,y-y0)=(0,0),∴x0=
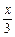 ,y0=
,y0=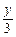 ,∴
,∴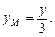 ∵
∵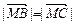 ,∴
,∴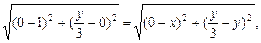
∴
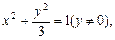 ∴顶点C的轨迹方程为
∴顶点C的轨迹方程为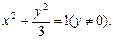 (4分)
(4分)(2)设直线l方程为:
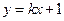 ,E(x1,y1),F(x2,y2),
,E(x1,y1),F(x2,y2),由
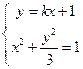 ,消去y得:
,消去y得: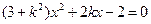 ①
①∴
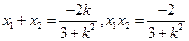 (6分)
(6分)∴
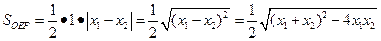 ,
,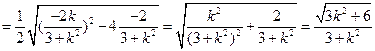
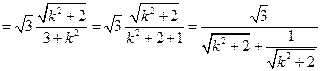 -----10分
-----10分设
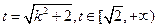 ,则
,则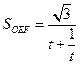 在
在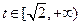 单调递减。
单调递减。故当
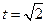 ,即
,即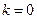 时,
时,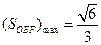 ----12分
----12分
练习册系列答案
相关题目
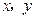 满足
满足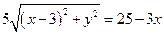 ,求
,求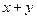 的最大值与最小值.
的最大值与最小值.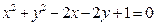 ,点
,点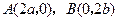 且
且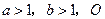 为坐标原点.
为坐标原点.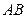 相切时,求
相切时,求 面积最小,求直线
面积最小,求直线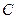 :
: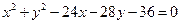 内有1点
内有1点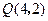 ,过
,过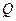 作直角
作直角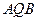 交圆于
交圆于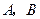 ,求动弦
,求动弦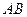 中点的轨迹方程.
中点的轨迹方程.
 轴弦长为2.(2)被
轴弦长为2.(2)被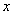 轴分成两段圆弧,其弧长之比为3:1在满足(1)(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长之比为3:1在满足(1)(2)的所有圆中,求圆心到直线 距离最小时圆的方程.
距离最小时圆的方程. , BC=
, BC=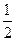 ,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足:
,椭圆E以A,B为焦点且经过点D. (1)建立适当的直角坐标系,求椭圆E的方程; (2)若点Q满足: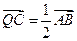 ,问是否存在不平行AB,的直线
,问是否存在不平行AB,的直线 与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线
与椭圆E交于M、N两点.且|MQ|=|NQ|.若存在,求直线 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.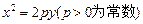 ,
,
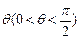 的直线交抛物线于
的直线交抛物线于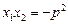
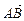 所成的比为
所成的比为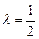 ,求直线AB的方程
,求直线AB的方程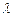 ,求
,求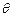 的函数关系式。
的函数关系式。 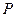 是曲线
是曲线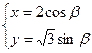 上一点,
上一点,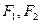 是该曲线的两个焦点,若
是该曲线的两个焦点,若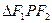 内角平分线的交点到三边上的距离为1,,则
内角平分线的交点到三边上的距离为1,,则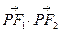 的值为
的值为