题目内容
条件:(1)截 轴弦长为2.(2)被
轴弦长为2.(2)被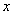 轴分成两段圆弧,其弧长之比为3:1在满足(1)(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长之比为3:1在满足(1)(2)的所有圆中,求圆心到直线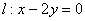 距离最小时圆的方程.
距离最小时圆的方程.
 轴弦长为2.(2)被
轴弦长为2.(2)被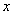 轴分成两段圆弧,其弧长之比为3:1在满足(1)(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长之比为3:1在满足(1)(2)的所有圆中,求圆心到直线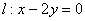 距离最小时圆的方程.
距离最小时圆的方程.设所求圆的方程为: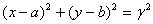 ,则由截
,则由截 轴的弦长为2得
轴的弦长为2得
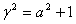
由被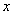 轴分成两段圆弦,其弧长之比为
轴分成两段圆弦,其弧长之比为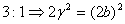 ,∴
,∴
圆心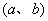 到直线
到直线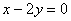 的距离
的距离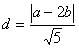
即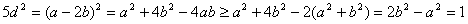
∴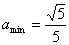 , 此时
, 此时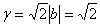
所以,所求圆的方程为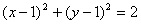 或
或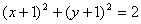
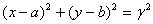 ,则由截
,则由截 轴的弦长为2得
轴的弦长为2得
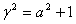
由被
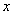 轴分成两段圆弦,其弧长之比为
轴分成两段圆弦,其弧长之比为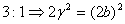 ,∴
,∴
圆心
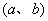 到直线
到直线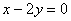 的距离
的距离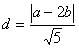
即
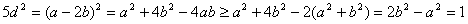
∴
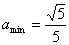 , 此时
, 此时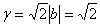
所以,所求圆的方程为
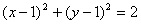 或
或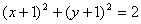
本题考查了用待定系数法求圆的方程,其中条件(1)和(2)的转化要注意利用圆的几何性质,只有这样才能既直观又准确地写出其代数关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
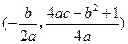 ,准线方程是
,准线方程是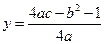 ,求证:抛物线的方程为
,求证:抛物线的方程为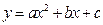 .
.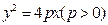 的准线与
的准线与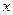 轴的交点为
轴的交点为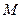 ,过点
,过点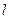 交抛物线于
交抛物线于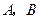 两点.
两点.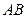 中点的轨迹方程;
中点的轨迹方程; 和双曲线
和双曲线 有公共的焦点,(1)求双曲线的渐近线方程(2)直线
有公共的焦点,(1)求双曲线的渐近线方程(2)直线 过焦点且垂直于x轴,若直线
过焦点且垂直于x轴,若直线 ,求双曲线的方程
,求双曲线的方程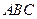 的两个顶点
的两个顶点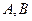 的坐标分别为
的坐标分别为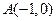 ,
,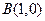 ,平面内两点
,平面内两点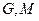 同时满足下列条件:①
同时满足下列条件:①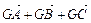 =0;②
=0;②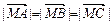 ;③
;③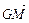 ∥
∥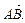 (1)求△
(1)求△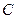 的轨迹方程;(2)过点
的轨迹方程;(2)过点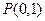 直线
直线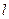 与(1)中轨迹交于不同的两点
与(1)中轨迹交于不同的两点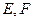 ,求△
,求△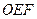 面积的最大值.
面积的最大值.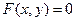 的点都在曲线
的点都在曲线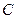 上,那么 ( )
上,那么 ( )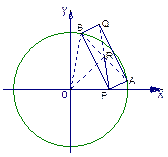
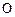 为坐标原点,点
为坐标原点,点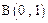 ,
, 且点
且点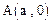
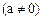 是
是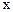 轴上动点,过点
轴上动点,过点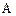 作线段
作线段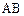 的
的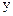 轴于点
轴于点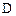 ,在直线
,在直线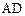 上取点
上取点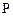 ,使
,使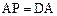 。
。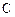 的方程;
的方程;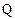 是直线
是直线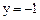 上的一个动点,
上的一个动点,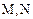 ,
,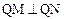
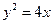 的焦点到准线的距离是 .
的焦点到准线的距离是 .