题目内容
下列命题是假命题的是( )
| A、?α,β∈R,使tan(α+β)=tanα+tanβ成立 | B、?α,β∈R,使cos(α+β)<cosα+cosβ成立 | C、△ABC中,“A<B”是“sinA<sinB”成立的充要条件 | D、?φ∈R,函数y=sin(2x+φ)都不是偶函数 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:举出正例α=β=0可判断A;举出正例α=β=
可判断B;
| π |
| 2 |
解答:解:当α=β=0时,tan(α+β)=tanα+tanβ成立,故A中?α,β∈R,使tan(α+β)=tanα+tanβ成立,正确;
当α=β=
时,cos(α+β)<cosα+cosβ成立,故B中?α,β∈R,使cos(α+β)<cosα+cosβ成立,正确;
A,B是△ABC的内角,当“A>B”?“a>b”?“2sinA•R>2sinB•R”?“sinA<sinB”(其中R为三角形外接圆半径),故,“A<B”是“sinA<sinB”成立的充要条件,正确
当φ=
时,y=sin(2x+φ)=cos2x为偶函数,故D中,?φ∈R,函数y=sin(2x+φ)都不是偶函数,错误;
故选:D
当α=β=
| π |
| 2 |
A,B是△ABC的内角,当“A>B”?“a>b”?“2sinA•R>2sinB•R”?“sinA<sinB”(其中R为三角形外接圆半径),故,“A<B”是“sinA<sinB”成立的充要条件,正确
当φ=
| π |
| 2 |
故选:D
点评:本题以命题的真假判断为载体,考查了存在性命题的真假判断,充要条件等知识点,难度不大,属于基础题.

练习册系列答案
相关题目
当x∈[-
,
]时,函数f(x)=sinx+
cosx的最大值与最小值分别是( )
| π |
| 2 |
| π |
| 2 |
| 3 |
| A、1,-1 | ||
B、1,-
| ||
| C、2,-2 | ||
| D、2,-1 |
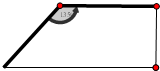 两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),则所用篱笆总长度的最小值为( )
两直立矮墙成135°二面角,现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园(墙足够长),则所用篱笆总长度的最小值为( )| A、16m | ||
| B、18m | ||
| C、22.5m | ||
D、15
|
定义“正对数”:ln+x=
,现有四个命题:
①若a>0,b>0,则ln+(ab)=bln+a
②若a>0,b>0,则ln+(ab)=ln+a+ln+b
③若a>0,b>0,则ln+(
)≥ln+a-ln+b
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2
其中正确的命题有( )
|
①若a>0,b>0,则ln+(ab)=bln+a
②若a>0,b>0,则ln+(ab)=ln+a+ln+b
③若a>0,b>0,则ln+(
| a |
| b |
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln2
其中正确的命题有( )
| A、①③④ | B、①②③ |
| C、①②④ | D、②③④ |
若p:φ=
+kπ,k∈Z,q:f(x)=sin(ωx+φ)(ω≠0)是偶函数,则p是q的( )
| π |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
已知椭圆C:
+
=1(a>b>0)的左、右焦点为F1、F2,离心率为
,过F2的直线l交C于A、B两点,若△AF1B的周长为4
,则C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=ex-ax-b,若f(x)≥0恒成立,则ab的最大值为( )
A、
| ||
| B、e2 | ||
| C、e | ||
D、
|