题目内容
已知函数f(x)=ex-ax-b,若f(x)≥0恒成立,则ab的最大值为( )
A、
| ||
| B、e2 | ||
| C、e | ||
D、
|
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:先求出函数的导数,再分别讨论a=0,a<0,a>0的情况,从而得出ab的最大值.
解答:解:f′(x)=ex-a,
若a=0,则f(x)=ex-b的最小值为f(-∞)=-b≥0,
得b≤0,此时ab=0;
若a<0,则f′(x)>0,函数单调增,此时f(-∞)=-∞,不可能恒有f(x)≥0.
若a>0,则得极小值点x=lna,由f(lna)=a-alna-b≥0,得b≤a(1-lna)
ab≤a2(1-lna)=g(a)
现求g(a)的最大值:由g'(a)=2a(1-lna)-a=a(1-2lna)=0,得极大值点a=e
g(e
)=
所以ab的最大值为
,
故选:D.
若a=0,则f(x)=ex-b的最小值为f(-∞)=-b≥0,
得b≤0,此时ab=0;
若a<0,则f′(x)>0,函数单调增,此时f(-∞)=-∞,不可能恒有f(x)≥0.
若a>0,则得极小值点x=lna,由f(lna)=a-alna-b≥0,得b≤a(1-lna)
ab≤a2(1-lna)=g(a)
现求g(a)的最大值:由g'(a)=2a(1-lna)-a=a(1-2lna)=0,得极大值点a=e
| 1 |
| 2 |
g(e
| 1 |
| 2 |
| e |
| 2 |
所以ab的最大值为
| e |
| 2 |
故选:D.
点评:本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
下列命题是假命题的是( )
| A、?α,β∈R,使tan(α+β)=tanα+tanβ成立 | B、?α,β∈R,使cos(α+β)<cosα+cosβ成立 | C、△ABC中,“A<B”是“sinA<sinB”成立的充要条件 | D、?φ∈R,函数y=sin(2x+φ)都不是偶函数 |
过双曲线C:
-
=1的右顶点做x轴的垂线,与C的一条渐近线相交于点A,若以C的右焦点为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=
x4-
x3+2x2+a在x=x1处取得极值2,则
dt=( )
| 1 |
| 4 |
| 4 |
| 3 |
| ∫ | 1 0 |
| a2-t2 |
A、π+
| ||||||||||||
| B、π | ||||||||||||
C、
| ||||||||||||
D、
|
依据表
下列选项中,哪一个样本所得的k值没有充分的证据显示“X与Y有关系”( )
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A、k=6.665 |
| B、k=3.765 |
| C、k=2.710 |
| D、k=2.700 |
若复数z=sinθ-
+(cosθ-
)i(i是虚数单位)是纯虚数,则tanθ值为( )
| 3 |
| 5 |
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
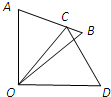 如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是
如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是