题目内容
一个球被成120°的二面角的两个半平面所截，截得的两个球的小圆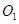
、
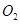相外切，
切点为二面角的棱上的同一点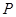
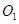，且圆和圆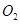半径分别为1和2，则球的表面积为
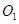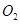、相外切，切点为二面角的棱上的同一点
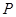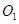，且圆和圆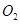半径分别为1和2，则球的表面积为A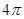． | B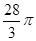． | C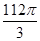． | D． |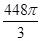
C
解：画出图形，如图，在四边形OMNA中，AM、AN是球的大圆的切线，
∴AM⊥OM，AN⊥ON，
∵∠MAN=120°∴∠MON=60°
∴两切点间的球面距离是 MN^=
∴OM=3，则此球的表面积是36π
故选C．
∴AM⊥OM，AN⊥ON，
∵∠MAN=120°∴∠MON=60°
∴两切点间的球面距离是 MN^=
∴OM=3，则此球的表面积是36π
故选C．
练习册系列答案
相关题目
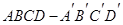中，
，
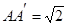，则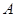
、
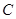两点间的球面距离是____
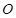为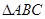
所在平面内一点，且
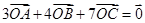,则
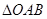和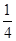
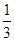
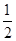
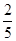
，一个球内切于该正方体，那么这个球的体积是（ ）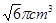
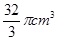
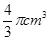
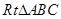中，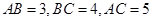
，将三角形绕AC边旋转一周所成的几何体的体积为________
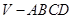中，底面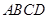
是边长为2的正方形，其它四个侧面都是侧棱长为
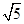的等腰三角形.
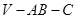的平面角的大小；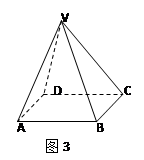
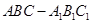的侧棱与底面边长都相等且为1，
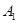在底面
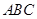内的射影为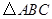
的中心，则三棱柱