题目内容
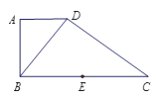
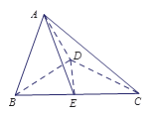
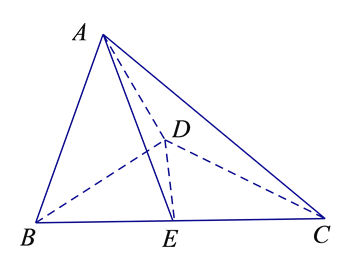
【题目】如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体.
(Ⅰ)求证:AB⊥平面ADC;
(Ⅱ)若AD=2,直线CA与平面ABD所成角的正弦值为![]() ,求二面角E-AD-C的余弦值.
,求二面角E-AD-C的余弦值.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】试题分析:(1)有平面![]() 平面
平面![]() ,证得
,证得![]() ,再根据线面垂直的判定定理,即可作出证明;
,再根据线面垂直的判定定理,即可作出证明;
(Ⅱ)现证得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,在
所成的角,在![]() 中,得到
中,得到![]() 的值,即可求解
的值,即可求解![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,利用空间向量即可求解二面角的大小.
,利用空间向量即可求解二面角的大小.
试题分析:(Ⅰ)证明:因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,
又DC⊥BD所以DC⊥平面ABD,所以DC⊥AB,
又AD⊥AB ,所以AB⊥平面ADC
(Ⅱ)因CD⊥平面ABD,所以∠CAD为直线CA与平面ABD所成的角,
CD⊥平面ABD所以CD⊥AD
则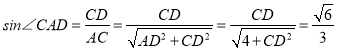
则![]() ,依题意得
,依题意得![]() 所以
所以![]() ,
,
即![]() ,所以
,所以![]()
取BD的中点O,连结AO,EO,因为![]() ,∴AO⊥BD,平面ABD⊥平面BCD,∴AO⊥平面BCD
,∴AO⊥BD,平面ABD⊥平面BCD,∴AO⊥平面BCD
如图所示建立空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由(1)可知AB⊥平面ADC,则平面ADC的法向量![]() ,
,
设平面ADE的法向量![]() ,
, ![]() ,
, ![]() ,
,
则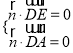 ,即
,即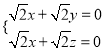 ,令
,令![]() ,得
,得![]() ,
, ![]()
所以![]() ,所以
,所以![]() ,
, ![]() ,由图可知二面角
,由图可知二面角![]() 为锐二面角,
为锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.