Question

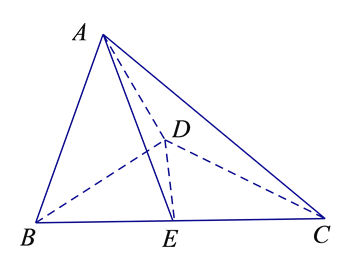
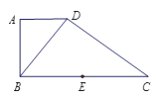
【题目】如图，在直角梯形中， // ， ⊥， ⊥, 点是边的中点, 将△沿折起，使平面⊥平面，连接, , , 得到如

图所示的空间几何体.

（Ⅰ）求证： ⊥平面；

（Ⅱ）若，求点到平面的距离.

Answer 1

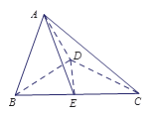
【答案】（I）详见解析；（II）.

【解析】试题分析：（I）先利用折叠前后的变和不变得到面面垂直和线线垂直，再利用面面垂直的性质和线面垂直的判定定理进行证明；（II）合理转化四面体的顶点，利用等体积法将点到平面的距离转化为求四面体的体积.

试题解析： (Ⅰ) 因为平面⊥平面，平面平面，

又⊥，所以⊥平面

因为平面，所以⊥

又⊥

∩

所以⊥平面.

(Ⅱ) ，.

依题意△～△，

所以，即.

故.

由于⊥平面，⊥, 为的中点,

得

同理

所以

因为⊥平面，所以.

设点到平面的距离为,

则,

所以，即点到平面的距离为.