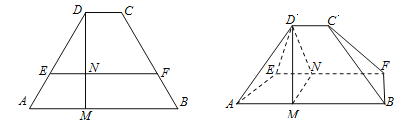题目内容
【题目】已知⊙![]() :
: ![]() 与⊙
与⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分别为左右焦点的椭圆
分别为左右焦点的椭圆![]() :
: ![]() 经过两圆的交点.
经过两圆的交点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,
的左右顶点, ![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上非顶点的三点,若
上非顶点的三点,若![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() 的面积为定值3..
的面积为定值3..
【解析】试题分析:(Ⅰ)依题意有![]() ,由椭圆定义知
,由椭圆定义知![]() ,解得
,解得![]() 点值,得出椭圆的方程;
点值,得出椭圆的方程;
(Ⅱ)由题可知![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,把直线
,把直线![]() 的方程为
的方程为![]() 与椭圆方程联立,利用根与系数的关系和韦达定理,即可求
与椭圆方程联立,利用根与系数的关系和韦达定理,即可求![]() 面积的定值.
面积的定值.
试题解析:(Ⅰ)设两圆的交点为![]() ,依题意有
,依题意有![]() ,
,
由椭圆定义知![]() ,解得
,解得![]() ;
;
因为![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左右焦点,所以
的左右焦点,所以![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)解法一 由题可知![]() ,
, ![]() ,设
,设![]() ,∵
,∵![]() 上的点,
上的点,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∵![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,∴
,∴![]() ,
,
∵![]() 、
、![]() 、
、![]() 是椭圆
是椭圆![]() 上非顶点的三点,∴直线
上非顶点的三点,∴直线![]() 的斜率存在且不为零,
的斜率存在且不为零,
设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
,
由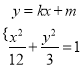 ,得
,得![]() ,
,
由![]() ,得
,得![]() (*)
(*)
且![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,整理得
,整理得![]() ,
,
代入(*)得![]() ,
,
∵
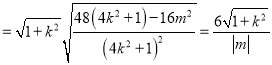 ,
,
原点![]() 到直线
到直线![]() 的距离
的距离![]() ,∴
,∴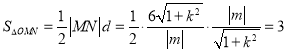 (定值).
(定值).
综上所述, ![]() 的面积为定值3.(Ⅱ)解法二 同解法一可知,直线
的面积为定值3.(Ⅱ)解法二 同解法一可知,直线![]() ,
, ![]() 的斜率存在且不为零,且
的斜率存在且不为零,且![]() ,……6分
,……6分
设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
, ![]() ,
,
由 得
得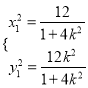 ,用
,用![]() 换
换![]() 可得
可得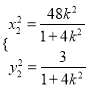 ,则
,则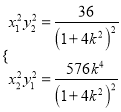 ,
,
因为![]() ,所以与
,所以与![]() 异号,
异号,
∴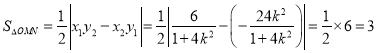 (定值).
(定值).
综上所述, ![]() 的面积为定值3.
的面积为定值3.

练习册系列答案
相关题目