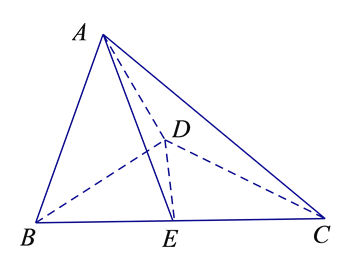
[题目]已知四棱锥的底面为平行四边形.且,, 分别为中点.过作平面分别与线段相交于点.(Ⅰ)在图中作出平面使面| ,(II)若.在(Ⅰ)的条件下求多面体的体积. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知四棱锥的底面为平行四边形，且,, 分别为中点，过作平面分别与线段相交于点.

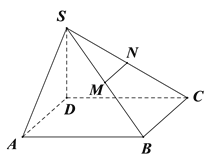
（Ⅰ）在图中作出平面使面‖ (不要求证明）；

（II）若，在（Ⅰ）的条件下求多面体的体积.

【答案】（Ⅰ）见解析;（Ⅱ）.

【解析】试题分析：（Ⅰ）利用面面平行的性质，只要即可.

（Ⅱ）利用体积分割法分别求体积，再求和

试题解析：（Ⅰ）如图，是的中点（若不是虚线，扣两分）

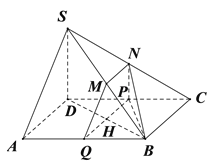
（Ⅱ）连接PB,NB，由题可知在（Ⅰ）情况下，

平面MNPQ与平面ABCD垂直，由题知AB=4，BC=PC=2，SD=2，NP=1

且面，则面

是边长为2的等边三角形则

由, ，面MNPQ是直角梯形， ,

连接交于点，在中，由余弦定理可知, 则，

即,且故

故

故此多面体的体积为

练习册系列答案

相关题目

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，直线的参数方程为（为参数，）.以原点为极点，以轴正半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系.设曲线的极坐标方程为.

（Ⅰ）设为曲线上任意一点，求的取值范围；

（Ⅱ）若直线与曲线交于两点，，求的最小值.

【题目】如图所示，有两个独立的转盘（）、（）．两个图中三个扇形区域的圆心角分别为、、．用这两个转盘进行玩游戏，规则是：依次随机转动两个转盘再随机停下（指针固定不会动，当指针恰好落在分界线时，则这次结果无效，重新开始），记转盘（）指针所对的数为，转盘（）指针所对的数为，（、），求下列概率：

（1）；

（2）．

【题目】已知幂函数f（x）=（﹣2m2+m+2）xm+1为偶函数．
（1）求f（x）的解析式；
（2）若函数y=f（x）﹣2（a﹣1）x+1在区间（2，3）上为单调函数，求实数a的取值范围．

【题目】某农科所发现，一种作物的年收获量（单位：）与它“相近”作物的株数具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 )，并分别记录了相近作物的株数为时，该作物的年收获量的相关数据如下：

（1）求该作物的年收获量关于它“相近”作物的株数的线性回归方程；

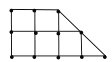
（2）农科所在如图所示的直角梯形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，图中

每个小正方形的边长均为，若从直角梯形地块的边界和内部各随机选取一株该作物，求这两株作物 “相

近”且年产量仅相差的概率．

附：对于一组数据，其回归直线的斜率和截距的最小二乘估

计分别为, ,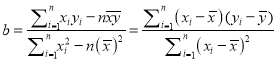

【题目】已知二次函数且，且，函数的图象与直线相切.

（1）求的解析式；

（2）若当时，恒成立，求实数的取值范围；

（3）是否存在区间，使得在区间上的值域恰好为？若存在，请求出区间，若不存在，请说明理由.

【题目】已知函数f（x）=loga（x+b）（其中a，b为常数，且a＞0，a≠1）的图象经过点A（﹣2，0），B（1，2）．
（1）求f（x）的解析式；
（2）若函数g（x）=（）2x﹣（）x﹣1，x∈[0，+∞），求g（x）的值域．

【题目】如图1，在直角梯形ABCD中，AD∥BC，AB⊥BC，BD⊥DC，点E是BC边的中点，将△ABD沿BD折起，使平面ABD⊥平面BCD，连接AE，AC，DE，得到如图2所示的几何体．

（Ⅰ）求证：AB⊥平面ADC；

（Ⅱ）若AD＝2，直线CA与平面ABD所成角的正弦值为，求二面角E－AD－C的余弦值．

【题目】已知f（x2﹣1）定义域为[0，3]，则f（2x﹣1）的定义域为

试题分类