题目内容
【题目】已知数列![]() 的各项均为正整数,Sn为其前n项和,对于n=1,2,3,…,有
的各项均为正整数,Sn为其前n项和,对于n=1,2,3,…,有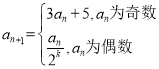 ,其中
,其中![]() 为使
为使![]() 为奇数的正整数,当
为奇数的正整数,当![]() 时,
时,![]() 的最小值为__________;当
的最小值为__________;当![]() 时,
时,![]() ___________.
___________.
【答案】5 910
【解析】
由题设可知当![]() 时,
时,![]() 解得
解得![]() 或
或![]() ,因为
,因为![]() 的各项均为正整数,
的各项均为正整数,![]() 为正整数,所以当
为正整数,所以当![]() 时,
时,![]() 有最小值
有最小值![]() .当
.当![]() 时,可求出
时,可求出![]() ,得到数列
,得到数列![]() 是周期为2的周期数列,可求出结果.
是周期为2的周期数列,可求出结果.
数列![]() 的各项均为正整数
的各项均为正整数
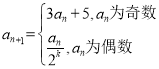 ,其中
,其中![]() 为使
为使![]() 为奇数的正整数.
为奇数的正整数.
当![]() 时,
时,![]() 或
或![]() .
.
即![]() 或
或![]() ,则
,则![]() 或
或![]() (舍)
(舍)
所以![]() 或
或![]() .
.
则![]() 或
或![]() ,因为
,因为![]() 的各项均为正整数,
的各项均为正整数,![]() 为正整数.
为正整数.
显然当![]() 时,
时,![]() 有最小值
有最小值![]() .
.
当![]() 时,
时,![]() ,
,
![]() ,其中
,其中![]() 为使
为使![]() 为奇数的正整数,所以
为奇数的正整数,所以![]() ,
,![]()
所以![]() ,
,
![]() ,其中
,其中![]() 为使
为使![]() 为奇数的正整数,所以
为奇数的正整数,所以![]() ,
,![]()
……………………
所以数列![]() 是周期为2的周期数列,奇数项为1,偶数项为8.
是周期为2的周期数列,奇数项为1,偶数项为8.
![]()
![]()
故答案为(1) 5 (2)910

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目