Question

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为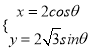（为参数），以坐标原点为极点， 轴的正半轴为极轴，与直角坐标系取相同的单位长度建立极坐标系，曲线的极坐标方程为.

（1）化曲线的方程为普通方程，并说明它们分别表示什么曲线；

（2）设曲线与轴的一个交点的坐标为，经过点作斜率为1的直线， 交曲线于两点，求线段的长.

Answer 1

【答案】（1）以为圆心，半径为的圆.（2）

【解析】试题分析：(1)利用三角恒等式消参化简 的方程即可，利用极坐标与直角坐标的关系，等式两侧乘以 即可将 的极坐标方程化简为直角坐标方程；(2)利用题意结合(1)中的结论求得点 的直角坐标，然后利用点到直线的距离公式求解距离即可.

试题解析：

（1）曲线的普通方程为，表示焦点在轴上的椭圆，

由，得，整理得，

即为曲线的普通方程，表示以为圆心，半径为的圆.

（2）令，得，所以，直线，

将曲线的参数方程代入直线方程得： ，

整理得，即，或，

所以， .