题目内容
【题目】设抛物线的顶点在坐标原点,焦点![]() 在
在![]() 轴上,过点
轴上,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,线段
两点,线段![]() 的长度为8,
的长度为8, ![]() 的中点到
的中点到![]() 轴的距离为3.
轴的距离为3.
(1)求抛物线的标准方程;
(2)设直线![]() 在
在![]() 轴上的截距为6,且抛物线交于
轴上的截距为6,且抛物线交于![]() 两点,连结
两点,连结![]() 并延长交抛物线的准线于点
并延长交抛物线的准线于点![]() ,当直线
,当直线![]() 恰与抛物线相切时,求直线
恰与抛物线相切时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】【试题分析】(1)依据题设条件,直接运用抛物线的定义分析求解;(2)依据题设建立直线方程,再与抛物线方程联立,借助坐标之间的关系,建立方程求解:
(1)设所求抛物线方程为![]() ,
,
则![]() ,又
,又![]() ,所以
,所以![]() .
.
即该抛物线的标准方程为![]() .
.
(2)由题意,直线![]() 的斜率存在,不妨设直线
的斜率存在,不妨设直线![]() ,
, ![]() ,
,
由![]() 消
消![]() 得
得![]() ,即
,即![]() (*)
(*)
抛物线在点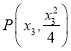 处的切线方程为
处的切线方程为![]() ,
,
令![]() ,得
,得![]() ,所以
,所以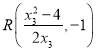 ,
,
而![]() 三点共线,所以
三点共线,所以![]() 及
及![]() ,得
,得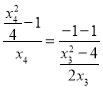 .
.
即![]() ,
,
整理得![]() ,
,
将(*)式代入上式得![]() ,即
,即![]() ,
,
所以所求直线![]() 的方程为
的方程为![]() .
.

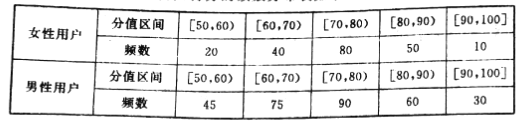
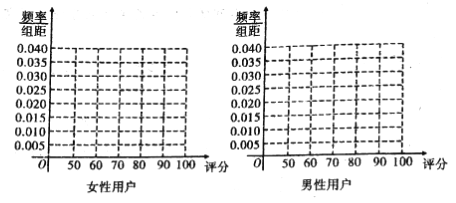
【题目】某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
A小区 | 低碳族 | 非低碳族 |
比例 |
|
|
B小区 | 低碳族 | 非低碳族 |
比例 |
|
|
C小区 | 低碳族 | 非低碳族 |
比例 |
|
|
(1)从A,B,C三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列.
【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数),现随机抽取20天的指数(见下表),将指数不低于![]() 视为当天空气质量优良.
视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
(1)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(2)以这20天的数据估计我市总体空气质量(天数很多),若从我市总体空气质量指数中随机抽取3天的指数,用![]() 表示抽到空气质量为优良的天数,求
表示抽到空气质量为优良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.