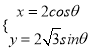题目内容
【题目】定义在 ![]() 上的函数
上的函数 ![]() 若同时满足:①存在
若同时满足:①存在 ![]() ,使得对任意的
,使得对任意的 ![]() ,都有
,都有 ![]() ;②
;② ![]() 的图象存在对称中心.则称
的图象存在对称中心.则称 ![]() 为“
为“![]() 函数”.已知函数
函数”.已知函数 ![]() 和
和 ![]() ,则以下结论一定正确的是
,则以下结论一定正确的是 ![]()
A. ![]() 和
和 ![]() 都是
都是 ![]() 函数 B.
函数 B. ![]() 是
是 ![]() 函数,
函数, ![]() 不是
不是 ![]() 函数
函数
C. ![]() 不是
不是 ![]() 函数,
函数, ![]() 是
是 ![]() 函数 D.
函数 D. ![]() 和
和 ![]() 都不是
都不是 ![]() 函数
函数
【答案】B
【解析】①存在M>0,使得对任意的x1,x2∈D,都有|f(x1)-f(x2)|<M函数f(x)在D上是“有界函数”.对于函数f1(x)=![]() =
=![]() ,定义域为R,∵2x>0,∴0<
,定义域为R,∵2x>0,∴0<![]()
![]() ,∴f1(x)∈(-1,1),∴满足①,又f1(-x)=
,∴f1(x)∈(-1,1),∴满足①,又f1(-x)=![]() ,∴函数f1(x)是奇函数,关于原点中心对称.∴f1(x)是“P-函数”.
,∴函数f1(x)是奇函数,关于原点中心对称.∴f1(x)是“P-函数”.
![]() 定义域为R,令x=tan
定义域为R,令x=tan![]() 则f2(x)=lg
则f2(x)=lg![]() ∴f2(x)
∴f2(x)![]() 不满足①,因此,f2(x)不是“P-函数”.
不满足①,因此,f2(x)不是“P-函数”.
故选B.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案【题目】环境监测中心监测我市空气质量,每天都要记录空气质量指数(指数采取10分制,保留一位小数),现随机抽取20天的指数(见下表),将指数不低于![]() 视为当天空气质量优良.
视为当天空气质量优良.
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
天数 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空气质量指数 |
|
|
|
|
|
|
|
|
|
|
(1)求从这20天随机抽取3天,至少有2天空气质量为优良的概率;
(2)以这20天的数据估计我市总体空气质量(天数很多),若从我市总体空气质量指数中随机抽取3天的指数,用![]() 表示抽到空气质量为优良的天数,求
表示抽到空气质量为优良的天数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】2016世界特色魅力城市![]() 强新鲜出炉,包括黄山市在内的
强新鲜出炉,包括黄山市在内的![]() 个中国城市入选. 美丽的黄山风景和人文景观迎来众多宾客. 现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了
个中国城市入选. 美丽的黄山风景和人文景观迎来众多宾客. 现在很多人喜欢自助游,某调查机构为了了解“自助游”是否与性别有关,在黄山旅游节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 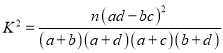
|
|
|
|
|
|
|
|
|
|