题目内容
【题目】公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形的面积可无限接近圆的面积，并创立了“割圆术”，利用“割圆术”，刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”，利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为（ ）
（参考数据： 
）
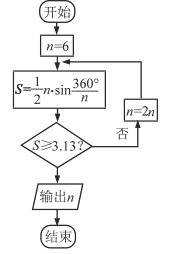
A. 12 B. 24 C. 48 D. 96
【答案】C
【解析】第1次执行循环体后,S=
×6×sin60=
，不满足退出循环的条件，则n=12，
第2次执行循环体后,S=
×12×sin30=3，不满足退出循环的条件，则n=24，
第3次执行循环体后,S=
×24×sin15≈3.1056，不满足退出循环的条件，则n=48，
第4次执行循环体后,S=
×48×sin7.5°≈3.132，满足退出循环的条件，
故输出的n值为48，
本题选择C选项.
练习册系列答案
相关题目
【题目】2016世界特色魅力城市
强新鲜出炉，包括黄山市在内的
个中国城市入选. 美丽的黄山风景和人文景观迎来众多宾客. 现在很多人喜欢自助游，某调查机构为了了解“自助游”是否与性别有关，在黄山旅游节期间，随机抽取了
人，得如下所示的列联表：
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
（1）若在
这人中，按性别分层抽取一个容量为
的样本，女性应抽
人，请将上面的列联表补充完整（在答题卡上直接填写结果，不需要写求解过程），并据此资料能否在犯错误的概率不超过
前提下，认为赞成“自助游”是与性别有关系？
（2）若以抽取样本的频率为概率，从旅游节游客中随机抽取
人赠送精美纪念品，记这
人中赞成“自助游”人数为
，求
的分布列和数学期望.
附: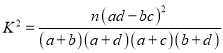 
|
|
|
|
|
|
|
|
|
|
