题目内容
【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线;
的轨迹方程,并说明其轨迹是什么曲线;
(3)是否存在实数![]() ,使得原
,使得原![]() 上有四点到直线
上有四点到直线![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
【答案】(1)见解析;(2)M的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆;(3)
为半径的圆;(3)![]() 或
或![]() .
.
【解析】【试题分析】(1)依据题设可以运用圆心与直线的距离或考虑动直线过定点分析判断;(2)借助题设条件运用圆心与弦中点的连线与直线垂直建立方程求解;(3)依据题设借助图形的直观,运用圆心距与直线的位置和数量关系建立不等式:
(1)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,所以圆心C到直线
,所以圆心C到直线![]() 的距离
的距离 .
.
所以直线![]() 与圆C相交,即直线
与圆C相交,即直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
或:直线![]() 的方程可化为
的方程可化为![]() ,无论m怎么变化,直线
,无论m怎么变化,直线![]() 过定点
过定点![]() ,由于
,由于![]() ,所以点
,所以点![]() 是圆C内一点,故直线
是圆C内一点,故直线![]() 与圆
与圆![]() 总有两个不同的交点.
总有两个不同的交点.
(2)设中点为![]() ,因为直线
,因为直线![]() 恒过定点
恒过定点![]() ,
,
当直线![]() 的斜率存在时,
的斜率存在时, ![]() ,又
,又![]() ,
, ![]() ,
,
所以![]() ,化简得
,化简得![]() .
.
当直线![]() 的斜率不存在时,中点
的斜率不存在时,中点![]() 也满足上述方程.
也满足上述方程.
所以M的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.
(3) 假设存在直线![]() ,使得圆上有四点到直线
,使得圆上有四点到直线![]() 的距离为
的距离为![]() ,由于圆心
,由于圆心![]() ,半径为
,半径为![]() ,则圆心
,则圆心![]() 到直线
到直线![]() 的距离为
的距离为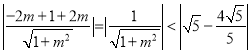
化简得![]() ,解得
,解得![]() 或
或![]() .
.

【题目】某公交公司为了方便市民出行、科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为研究车辆发车间隔时间![]() (分钟)与乘客等候人数
(分钟)与乘客等候人数![]() (人)之间的关系,经过调查得到如下数据:
(人)之间的关系,经过调查得到如下数据:
间隔时间 |
|
|
|
|
|
|
等候人数 |
|
|
|
|
|
|
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过
的差,若差值的绝对值不超过![]() ,则称所求线性回归方程是“恰当回归方程”.
,则称所求线性回归方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间之差大于
组数据的间隔时间之差大于![]() 的概率;
的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)在(2)的条件下,为了使等候的乘客不超过![]() 人,则间隔时间最多可以设置为多少分钟?(精确到整数)
人,则间隔时间最多可以设置为多少分钟?(精确到整数)
参考公式: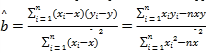 ,
,![]() .
.
