Question

【题目】命题：方程表示焦点在轴上的双曲线：命题：若存在，使得成立.

（1）如果命题是真命题，求实数的取值范围；

（2）如果“”为假命题，“”为真命题，求实数的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】

（1）由方程表示焦点在轴上的双曲线，得到，即可求解；

（2）由（1）中命题为真命题时，得到，再求得命题为真命题，得到，结合“”为假命题，“”为真命题，得、两个命题一真一假，分类讨论，即可求解.

（1）由题意，方程表示焦点在轴上的双曲线，

则满足，解得，

即命题为真命题时，实数的取值范围是.

（2）若命题为真命题，则在有解，解得，

又由“”为假命题，“”为真命题，则、两个命题一真一假，

若真假，则，解得；

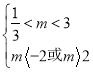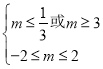若假真，则，解得，

综上，实数的取值范围为.