Question

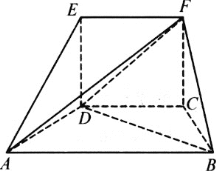
【题目】如图所示，曲线C由部分椭圆C1：＋＝1（a>b>0，y≥0）和部分抛物线C2：y＝－x2＋1（y≤0）连接而成，C1与C2的公共点为A，B，其中C1所在椭圆的离心率为．

（1）求a，b的值；

（2）过点B的直线l与C1，C2分别交于点P，Q（P，Q，A，B中任意两点均不重合），若AP⊥AQ，求直线l

的方程．

Answer 1

【答案】（1），；（2）．

【解析】

试题（1）结合图形在中，令，得，再联立， 可得，，；（2）由题易得点，，由题知直线与轴不重合也不垂直，可设其方程为（），联立的方程，整理得，解得点的坐标为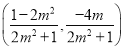，结合图形知，再将代入的方程，得点的坐标为，再由，即得，求得方程．

试题解析：（1）在C2的方程中令y＝0可得b＝1，由＝及a2－c2＝b2＝1得a＝，∴a＝,b＝1．

（2）由（1）知，上半椭圆C1的方程为y2＋2x2＝2（y≥0）．易知，直线l与x轴不重合也不垂直，

设其方程为x=my+1 （m≠0），并将其代入C1的方程，

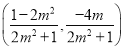整理得（2m2＋1）＋4my＝0，故可解得点P的坐标为，显然，m<0，

同理，将x=my+1 （m≠0）代入C2的方程,整理得m2y2＋y+2my＝0，得点Q的坐标为．

∵AP⊥AQ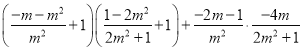，∴=0，

即8m2 +2m＝0，解得m＝－，符合m<0，故直线l的方程为4x+y－4＝0．