题目内容
【题目】将编号为1、2、3、4的四个小球随机的放入编号为1、2、3、4的四个纸箱中，每个纸箱有且只有一个小球，称此为一轮“放球”．设一轮“放球”后编号为
的纸箱放入的小球编号为
，定义吻合度误差为
(1) 写出吻合度误差
的可能值集合；
(2) 假设
等可能地为1，2，3，4的各种排列，求吻合度误差
的分布列；
(3)某人连续进行了四轮“放球”，若都满足
，试按(Ⅱ)中的结果，计算出现这种现象的概率(假定各轮“放球”相互独立)；
【答案】(1) 
.(2) 见解析(3) 
【解析】试题分析：（1）根据题意知
与
的奇偶性相同，误差
只能是偶数，由此写出
的可能取值；（2）用列举法求出基本事件数，利用古典概型概率公式计算对应的概率值，写出随机变量
的分布列；（3）利用互斥事件的概率公式计算
，再利用对立事件的概率公式求解.
试题解析：(1) 由于在1、2、3、4中奇数与偶数各有两个，所以
中的奇数的个数与
中偶数的个数相同．因此， 
与
的奇偶性相同，从而吻合度误差
只能是偶数，又因为
的值非负且值不大于8．因此，吻合度误差
的可能值集合
.
(2)用
表示编号为1、2、3、4的四个纸箱中放入的小球编号分别为
，则所有可能的结果如下:
易得
， 
， 
，
， 
于是，吻合度误差
的分布列如下:
| 0 | 2 | 4 | 6 | 8 |
|
|
|
|
|
|
(3)首先， 
由上述结果和独立性假设，可得出现这种现象的概率为
【题目】某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求y关于t的线性回归方程；
（2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
， 
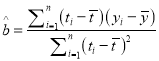