题目内容
15．已知复数z=$\frac{（1+i）2+3（1-i）}{2+i}$则z的共轭复数$\overline{z}$=1+i．分析 利用复数的分母实数化后，求解共轭复数即可．
解答 解：复数z=$\frac{（1+i）2+3（1-i）}{2+i}$=$\frac{5-i}{2+i}$=$\frac{（5-i）（2-i）}{（2+i）（2-i）}$=1-i．
z=$\frac{（1+i）2+3（1-i）}{2+i}$则z的共轭复数$\overline{z}$=1+i．
故答案为：1+i．
点评 本题考查复数的除法运算法则的应用，共轭复数的求法，基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
20．函数f（x）=2x3-4x 的单调递减区间是（ ）
| A． | （-$\sqrt{6}$，$\sqrt{6}$） | B． | （-$\frac{\sqrt{2}}{3}$，$\frac{\sqrt{2}}{3}$） | C． | （-$\frac{\sqrt{6}}{3}$，$\frac{\sqrt{6}}{3}$） | D． | （-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$） |
7．下列说法中正确的是（ ）
| A． | 若a＞b，则$\sqrt{a}$＞$\sqrt{b}$ | B． | 若|a|＞b，则a2＞b2 | C． | 若a＞b，则a2＞b2 | D． | 若a＞|b|，则a2＞b2 |
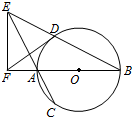如图AB是⊙O的直径，弦BD，CA的延长线相交于点E，EF垂直BA的延长线于点F．