题目内容
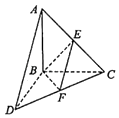
【题目】在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点. 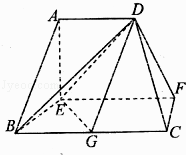
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的正弦值.
【答案】
(1)证明:∵AD∥EF,EF∥BC,∴AD∥BC,
∵BC=2AD,G为BC的中点,∴AD∥BG,且AD=BG,∴四边形ABCD是平行四边形,∴AB∥DG
因为AB不在平面DEG中,DG在平面DEG内,∴AB∥平面DEG
(2)证明:∵EF⊥平面AEB,AE平面AEB,BE平面AEB,
∴EF⊥AE,EF⊥BE,∵AE⊥EB,∴EB、EF、EA两两垂直.
以点E为坐标原点,EB、EF、EA所在直线分别为x、y、z轴建立空间直角坐标系,
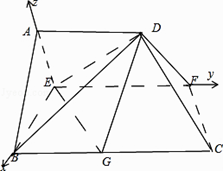
由已知得:A(0,0,2),B(2,0,0),C(2,4,0),D(0,2,2),F(0,3,0),G(2,2,0).
∵ ![]() ,∴
,∴ ![]()
∴BD⊥EG.
(3)解:由已知得 ![]() 是平面EFDA的法向量,设平面DCF的法向量为
是平面EFDA的法向量,设平面DCF的法向量为 ![]()
∵ ![]() ,∴
,∴ ![]() ,令z=1,得x=﹣1,y=2,即
,令z=1,得x=﹣1,y=2,即 ![]() .
.
设二面角C﹣DF﹣E的大小为θ,
则 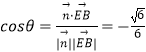 ,∴
,∴ ![]()
∴二面角C﹣DF﹣E的正弦值为 ![]() .
.
【解析】(1)要证AB∥平面DEG,可在平面DEG中找到一条直线与AB平行,根据题目给出的条件,能够证得AB∥DG;(2)根据题目条件先证明EB、EA、EF两两相互垂直,然后以E为原点,以EB、EF、EA所在直线分别为x、y、z轴建立空间直角坐标系,运用向量数量积等于0 ![]() ,从而证明BD⊥EG;(3)在(2)的基础上,求出二面角的两个半平面的法向量,利用法向量求二面角的平面角的余弦值.
,从而证明BD⊥EG;(3)在(2)的基础上,求出二面角的两个半平面的法向量,利用法向量求二面角的平面角的余弦值.

练习册系列答案
相关题目