题目内容
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.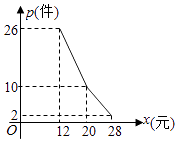
【答案】解:(I)当x∈[12,20]时,P=k1x+b1,代入点(12,26),(20,10)得k1=﹣2,b1=50,∴P=﹣2x+50;同理x∈(20,28]时,P=﹣x+30,
∴周销量P(件)与单价x(元)之间的函数关系式P= ![]() ;
;
(Ⅱ)y=P(x﹣10)﹣25= ![]() ,
,
当x∈[12,20]时,y= ![]() ,x=
,x= ![]() 时,ymax=
时,ymax= ![]() ;
;
当x∈(20,28]时,y=﹣(x﹣20)2+75,函数单调递减,∴y<75,
综上所述,x= ![]() 时,ymax=
时,ymax= ![]() .
.
【解析】(I)由图象可得当x∈[12,20]时,P=k1x+b1解得k1=﹣2,b1=50,∴P=﹣2x+50。当x∈(20,28]时,P=﹣x+30,即得周销量P(件)与单价x(元)之间的函数关系式。
(Ⅱ)由二次函数求最值得。当x∈[12,20]时,y= 2 ( x ![]() ) 2 +
) 2 +![]() ,x=
,x= ![]() 时,ymax=
时,ymax= ![]() ;当x∈(20,28]时,y=﹣(x﹣20)2+75,函数单调递减,∴y<75.
;当x∈(20,28]时,y=﹣(x﹣20)2+75,函数单调递减,∴y<75.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目