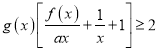题目内容
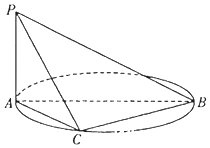
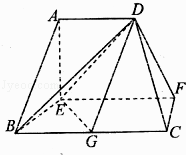
【题目】如图,三棱锥A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分别为MN的中点.
,∠ACB=45°,E,F分别为MN的中点. 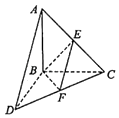
(1)求证:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
【答案】
(1)证明:连接E,F,
∵E,F分别为AC,CD的中点,∴EF∥AD,
又AD平面ADB,EF平面ADB,∴EF∥面ABD
(2)解:取BC中点G,过点G作BF的垂线GH,点H为垂足,
∵AB=4,AC=4 ![]() ,∠ACB=45°,
,∠ACB=45°,
∴由AB2=AC2+BC2﹣2ACBCcos45°,得16=32+BC2﹣8BC,即BC=4.
∴AB2+BC2=AC2,即AB⊥BC,
又平面ABC⊥平面BCD,且平面ABC∩平面BCD=BC,
∴AB⊥平面BCD,则EG⊥平面BCD,EG⊥BF,
又GH⊥BF,∴BF⊥平面EGH,则BF⊥EH,即∠EHG为二面角E﹣BF﹣C的平面角.
∵BD=4,BC=4,CD=4 ![]() ,∴BF=
,∴BF= ![]() .
.
则∠CBF=60°,∴GH=2× ![]() .
.
Rt△EGH中, ![]() .
.

【解析】(1)连接E,F,由E,F分别为AC,CD的中点,结合三角形中位线定理可得EF∥AD,再由线面平行的判定可得EF∥平面ABD;(2)由已知求解三角形可得AB⊥BC,结合△ABC和△BCD所在平面互相垂直可得AB⊥平面BCD,取BC中点G,过点G作BF的垂线GH,点H为垂足,则∠EHG为二面角E﹣BF﹣C的平面角,求解直角三角形得答案.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

【题目】某种零件按质量标准分为1,2,3,4,5五个等级,现从批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 | 1 | 2 | 3 | 4 | 5 |
频率 | 0.05 | m | 0.15 | 0.35 | n |
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n的值;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级不相同的概率.