题目内容
6.已知椭圆 C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),直线l与椭圆C有唯一公共点M,为坐标原点),当点M坐标为$({\sqrt{3},\frac{1}{2}})$时,l的方程为$\sqrt{3}$x+2y-4=0.(I)求椭圆C方程;
(Ⅱ)设直线l的斜率为K,M在椭圆C上移动时,作OH⊥l于H(O为坐标原点),求∠HOM最大时k的值.
分析 (Ⅰ)将M点坐标代入椭圆方程,同时联立直线l与椭圆方程,计算即得结论;
( II)通过设直线l并与椭圆方程联立,利用△=0,进而可得|OM|2、|OH|2的表达式,化简即得结论.
解答 解:(Ⅰ)由题意可得:$\frac{3}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$=1,(*)
将$\sqrt{3}$x+2y-4=0代入椭圆C,有:
(3a2+4b2)x2-8$\sqrt{3}$a2x+16a2-4a2b2=0,
令△=0得:3a2+4b2=16,(**)
联立(*)、(**),解得:a2=4,b2=1,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}$+y2=1;
( II)设直线l:y=kx+m,M(x0,y0).
将直线l的方程代入椭圆C得:(1+4k2)x2+8kmx+4m2-4=0,
令△=0,得m2=4k2+1,且${{x}_{0}}^{2}$=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$,
∴|OM|2=$\frac{1+16{k}^{2}}{1+4{k}^{2}}$,
又|OH|2=$\frac{{m}^{2}}{1+{k}^{2}}$=$\frac{1+4{k}^{2}}{1+{k}^{2}}$,
∴(cos∠HOM)2=$\frac{(1+4{k}^{2})^{2}}{(1+16{k}^{2})(1+{k}^{2})}$,
∵(1+16k2)(4+4k2)≤$\frac{(5+20{k}^{2})^{2}}{4}$=$\frac{25(1+4{k}^{2})^{2}}{4}$,
∴$\frac{(1+4{k}^{2})^{2}}{(1+16{k}^{2})(1+{k}^{2})}$≥$\frac{16}{25}$,等号当且仅当k2=$\frac{1}{4}$时成立,
∴∠HOM取最大时k=±$\frac{1}{2}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

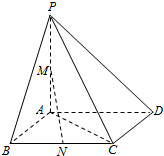 如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点
如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点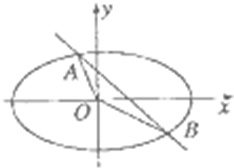 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.