题目内容
1.已知椭圆C的中心为原点,焦点F1,F2在x轴上,其离心率为$\frac{\sqrt{2}}{2}$,且过点($\frac{\sqrt{2}}{2},\frac{1}{2}$).(1)求椭圆C的标准方程;
(2)已知椭圆mx2+ny2=1在其上一点(x0,y0)处的切线方程是mx0x+ny0y=1,P是椭圆C上任意一点,在点P处作椭圆C的切线l,F1,F2到l的距离分别为d1,d2.探究:d1•d2是否为定值?若是,求出定值;若不是说明理由;
(3)求(2)中d1+d2的取值范围.
分析 (1)由题意,设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),运用离心率公式和点满足椭圆方程,解方程即可得到椭圆C的标准方程;
(2)由椭圆C方程为x2+2y2=1,求得焦点,设P(s,t),则l的方程是sx+2ty=1,求出d1•d2,结合s2+2t2=1,即可得出结论;
(3)先化简d1+d2,再求d1+d2的取值范围.
解答 解:(1)由题意,设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
由于椭圆过点($\frac{\sqrt{2}}{2},\frac{1}{2}$),
则$\frac{1}{2{a}^{2}}$+$\frac{1}{4{b}^{2}}$=1,又a2-b2=c2,
解得a=1,b=$\frac{\sqrt{2}}{2}$,
故所求为x2+$\frac{{y}^{2}}{\frac{1}{2}}$=1;
(2)椭圆C方程为x2+2y2=1,即有F1(-$\frac{\sqrt{2}}{2}$,0),F2($\frac{\sqrt{2}}{2}$,0),
设P(s,t),则切线l的方程是sx+2ty=1,
则d1d2=$\frac{|-\frac{\sqrt{2}}{2}s-1|•|-\frac{\sqrt{2}}{2}s-1|}{\sqrt{{s}^{2}+4{t}^{2}}•\sqrt{{s}^{2}+4{t}^{2}}}$=$\frac{|1-\frac{1}{2}{s}^{2}|}{{s}^{2}+4{t}^{2}}$,
因为-1≤s≤1,所以1-s2>0,
故d1d2=$\frac{1-\frac{1}{2}{s}^{2}}{{s}^{2}+4{t}^{2}}$,
又因为s2+2t2=1,
代入可得d1d2=$\frac{1}{2}$,
故d1•d2为定值$\frac{1}{2}$;
(3)由题d1+d2=$\frac{|-\frac{\sqrt{2}}{2}s-1|}{\sqrt{{s}^{2}+4{t}^{2}}}$+$\frac{|\frac{\sqrt{2}}{2}s-1|}{\sqrt{{s}^{2}+4{t}^{2}}}$
=$\frac{1+\frac{\sqrt{2}}{2}s+1-\frac{\sqrt{2}}{2}s}{\sqrt{{s}^{2}+4{t}^{2}}}$=$\frac{2}{\sqrt{{s}^{2}+4{t}^{2}}}$=$\frac{2}{\sqrt{1+2{t}^{2}}}$,
因为0≤t2$≤\frac{1}{2}$,所以d1+d2∈[$\sqrt{2}$,2].
点评 本题考查椭圆方程,考查点到直线距离公式的运用,考查学生分析解决问题的能力,属于中档题.

| A. | $(-∞,\frac{1}{2}]$ | B. | $[{\frac{1}{5},\frac{1}{2}}]$ | C. | $[{\frac{1}{5},+∞})$ | D. | $(-∞,\frac{1}{5}]$ |
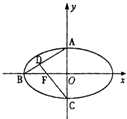 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.