题目内容

3．已知等差数列{an}中，a4+a8+a10+a14=20，则前17项的和为85．

分析 由已知结合等差数列的性质求得a1+a17，然后代入等差数列的前n项和得答案．

解答 解：在等差数列{an}中，由a4+a8+a10+a14=20，得2（a1+a17）=20，
∴a1+a17=10，
则${S}_{17}=\frac{（{a}_{1}+{a}_{17}）×17}{2}=\frac{10×17}{2}=85$．
故答案为：85．

点评 本题考查等差数列的性质，考查了等差数列的前n项和，是基础的计算题．

练习册系列答案
相关题目
6．已知椭圆 C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0），直线l与椭圆C有唯一公共点M，为坐标原点），当点M坐标为$（{\sqrt{3}，\frac{1}{2}}）$时，l的方程为$\sqrt{3}$x+2y-4=0．
（I）求椭圆C方程；
（Ⅱ）设直线l的斜率为K，M在椭圆C上移动时，作OH⊥l于H（O为坐标原点），求∠HOM最大时k的值．
7．若E，F，G，H分别在四面体的棱AB，BC，CD，AD上，且AC∥平面EFGH，则（　　）
A．EF∥GHB．EH∥FGC．EH∥平面BCDD．FG∥平面ABD
4．已知a＞b，ab≠0，则下列不等式中：①a2＞b2；②$\frac{1}{a}＜\frac{1}{b}$；③a3＞b3；④a2+b2＞2ab，恒成立的不等式的个数是（　　）
A．1个B．2个C．3个D．4个
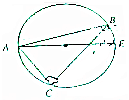11．若关于x的方程$\sqrt{3}$sinx+|cosx|+a=0在区间[0，2π]内有四个不同的解分别为x1，x2，x3，x4，则x1+x2+x3+x4的值为2π．
8．如图，已知，AE是⊙O的直径，弦BC与AE相交于D，求证：tanB•tanC=$\frac{AD}{DE}$．
15．观察下列各式：
sin245°+cos275°+sin45°cos75°=$\frac{3}{4}$，
sin240°+cos270°+sin40°cos70°=$\frac{3}{4}$，
sin210°+cos240°+sin10°cos40°=$\frac{3}{4}$
（1）分析上述各式的共同特点，写出能反映一般规律的等式；
（2）并对（1）的等式的正确性作出证明．
12．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点为F1，F2，若双曲线C上存在一点P，使得△PF1F2为等腰三角形，且cos∠F1PF2=$\frac{1}{4}$，则双曲线C的离心率为（　　）
A．$\frac{4}{3}$B．$\frac{3}{2}$C．2D．3
13．在（1-2x）7的展开式中，求：
（1）二项式系数的和；
（2）各项系数的和；
（3）奇数项的二项式系数和与偶数项的二项式系数和；
（4）奇数项系数和与偶数项系数和．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网