题目内容
P为抛物线y2=2px上任一点,F为焦点,则以PF为直径的圆与y轴( )
| A.相交 | B.相切 |
| C.相离 | D.位置由P确定 |
根据题意,可得抛物线y2=2px的焦点为F(
,0),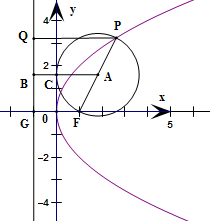
设P(m,n),PF的中点为A(x1,y1),
可得x1=
(
+m),
过P作准线l:x=-
的垂线,垂足为Q如图所示.
由抛物线的定义,得|PF|=|PQ|=m+
,
∴x1=
|PF|,即点A到y轴的距离等于以PF为直径的圆的半径.
因此,以PF为直径的圆与y轴相切.
故选:B
| p |
| 2 |
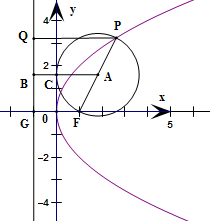
设P(m,n),PF的中点为A(x1,y1),
可得x1=
| 1 |
| 2 |
| p |
| 2 |
过P作准线l:x=-
| p |
| 2 |
由抛物线的定义,得|PF|=|PQ|=m+
| p |
| 2 |
∴x1=
| 1 |
| 2 |
因此,以PF为直径的圆与y轴相切.
故选:B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目