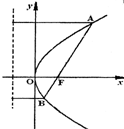
题目内容
抛物线y2=-12x的准线与双曲线
-
=1的两条渐近线所围成的三角形的面积等于( )
| x2 |
| 9 |
| y2 |
| 3 |
A.3
| B.2
| C.2 | D.
|
∵抛物线方程为y2=-12x,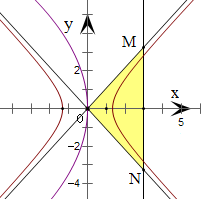
∴抛物线的焦点为F(-3,0),准线为x=3.
又∵双曲线
-
=1中,a=3且b=
,
∴双曲线的渐近线方程为y=±
x,即y=±
x.
∵直线x=3与直线y=±
x相交于点M(3,
),N(3,-
),
∴三条直线围成的三角形为△MON,以MN为底边、O到MN的距离为高,
可得其面积为S=
×|MN|×3=
×[
-(-
)]×3=3
.
故选:A

∴抛物线的焦点为F(-3,0),准线为x=3.
又∵双曲线
| x2 |
| 9 |
| y2 |
| 3 |
| 3 |
∴双曲线的渐近线方程为y=±
| b |
| a |
| ||
| 3 |
∵直线x=3与直线y=±
| ||
| 3 |
| 3 |
| 3 |
∴三条直线围成的三角形为△MON,以MN为底边、O到MN的距离为高,
可得其面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
故选:A

练习册系列答案
相关题目