题目内容
10.为举办校园文化节,某班推荐2名男生3名女生参加文艺技能培训,培训项目及人数分 别为:乐器1人,舞蹈2人,演唱2人,每人只参加一个项目,并且舞蹈和演唱项目必须 有女生参加,則不同的推荐方案的种数为24.(用数字作答)分析 依题意可分为两类:1类是乐器项目女生参加,2类是乐器项目男生参加,根据分类计数原理得到答案.
解答 解:依题意可分为两类:1类是乐器项目女生参加,则方法有${A}_{3}^{3}$$•{A}_{2}^{2}$=12种;
2类是乐器项目男生参加,方法有${C}_{2}^{1}•$(${C}_{3}^{2}$+${C}_{3}^{2}$)=12种,
根据分类计数原理,共有12+12=24种.
故答案为:24.
点评 本题考查了排列组合的意义及其计算公式、分类讨论的思想方法,属于基础题

练习册系列答案
相关题目
3.若集合A={x|2${\;}^{{x}^{2}-4x-5}$>1},集合B={x|y=lg$\frac{2-x}{2+x}$},则A∩B=( )
| A. | {x|-5<x<1} | B. | {x|-2<x<1} | C. | {x|-2<x<-1} | D. | {x|-5<x<-1} |
15.已知全集U=R,集合A={x|-2≤x<3},B={y|y=2x-1,x≥0},则A∩∁UB=( )
| A. | {x|-2≤x<0} | B. | $\left\{{x\left|{-2≤x<\frac{1}{2}}\right.}\right\}$ | C. | $\left\{{x\left|{0≤x<\frac{1}{2}}\right.}\right\}$ | D. | {x|0≤x<3} |
20.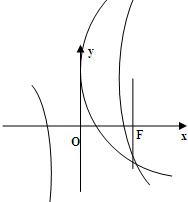 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
 如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
如图,已知抛物线是的焦点F恰好是双曲线$\frac{x^2}{a^2}$-$\frac{{y{\;}^2}}{b^2}$=1的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )| A. | $\sqrt{2}$+1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
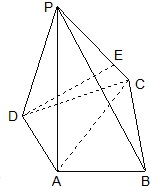 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.