题目内容
18．已知椭圆C：$\frac{x^2}{4}+\frac{y^2}{3}$=1，以坐标原点为极点，x轴正半轴为极轴建立极坐标系（取同样单位长度），直线l的极坐标方程为ρcos（θ+$\frac{π}{3}$）═-$\frac{9}{2}$．（Ⅰ）写出椭圆C的参数方程及直线l的直角坐标方程；
（Ⅱ）求椭圆C上的点P到直线l的距离的最大值．
分析 （I）利用sin2α+cos2α=1即可把曲线C的普通方程化为参数方程；利用x=ρcosθ，y=ρsinθ，可得直线l的直角坐标方程；
（II）设与直线l平行且与椭圆相切的直线方程，与椭圆方程联立，令△=0，解得m，求出两条平行线之间的距离即可．
解答 解：（I）利用sin2α+cos2α=1，可得圆C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=\sqrt{3}sinα}\end{array}\right.$；
ρcos（θ+$\frac{π}{3}$）=-$\frac{9}{2}$，可化为$\frac{1}{2}$ρcosθ-$\frac{\sqrt{3}}{2}$ρsinθ=-$\frac{9}{2}$，
∴直线l的直角坐标方程为x-$\sqrt{3}$y+9=0；
（II）设与直线l平行且与椭圆相切的直线方程为x-$\sqrt{3}$y+m=0，
与椭圆方程联立，化为$13{y}^{2}-6\sqrt{3}my+3{m}^{2}-12=0$，
令△=0，化为m2=13，解得m=±$\sqrt{13}$．
取m=$\sqrt{13}$，
则M到直线l的距离的最大值$\frac{9-\sqrt{13}}{2}$．
点评 本题主要考查曲线的参数方程与极坐标方程、直线的极坐标方程、直线与椭圆相切问题、平行线之间的距离等基础知识，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
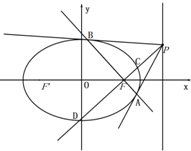已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，以原点为圆心，以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切．
10．sin$\frac{5π}{12}$=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |