题目内容
14.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的中心为O,右顶点为A,在线段OA上任意选定一点M(m,0)(0<m<2),过点M作与x轴垂直的直线交C于P,Q两点.(Ⅰ)若椭圆C的长半轴为2,离心率$\frac{{\sqrt{2}}}{2}$,
(ⅰ)求椭圆C的标准方程;
(ⅱ)若m=1,点N在OM的延长线上,且|OM|,|OA|,|ON|成等比数列,试证明直线PN与C相切;
(Ⅱ)试猜想过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上一点G(x0,y0)(x0>0,y0>0)的切线方程,再加以证明.
分析 (Ⅰ)(ⅰ)运用椭圆的离心率公式和a,b,c的关系,计算即可得到椭圆方程;
(ⅱ)运用等比数列的性质,求得P,N的坐标,求出直线PN的方程,代入椭圆方程,计算判别式,即可得到直线PN与C相切;
(Ⅱ)在x轴上取点$N(\frac{a^2}{x_0},0)$,连结GN,则直线GN为点G处的切线方程.设直线GN的方程为:$y=k(x-\frac{a^2}{x_0})$,代入椭圆方程,计算判别式为0,即可得到切线方程.
解答 解:(Ⅰ)(ⅰ)因为$a=2,e=\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,
所以a=2,c=$\sqrt{2}$,b=$\sqrt{2}$,
所以椭圆C的标准方程为:$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(ⅱ)由已知条件得:|OM|=1,|OA|=2,
设P(1,y),则${y^2}=\frac{3}{2}$,所以$P(1,±\frac{{\sqrt{6}}}{2})$.
因为|OM|,|OA|,|ON|成等比数列,
所以|OA|2=|OM||ON|,即$|{ON}|=\frac{{{{|{OA}|}^2}}}{{|{OM}|}}=4$,所以N(4,0).
直线PN的方程为:$y=±\frac{{\sqrt{6}}}{6}(x-4)$代入椭圆$C:\frac{x^2}{4}+\frac{y^2}{2}=1$,
整理得:x2-2x+1=0.
因为△=4-4=0,
所以直线PN与C相切.
(Ⅱ)在x轴上取点$N(\frac{a^2}{x_0},0)$,连结GN,则直线GN为点G处的切线方程.
证明:设直线GN的方程为:$y=k(x-\frac{a^2}{x_0})$(其中$k=\frac{y_0}{{{x_0}-\frac{a^2}{x_0}}}=\frac{{{x_0}{y_0}}}{{x_0^2-{a^2}}}$),
把$y=k(x-\frac{a^2}{x_0})$代入$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
整理得:$({b^2}+{a^2}{k^2}){x^2}-\frac{{2{a^4}{b^2}}}{x_0}x+\frac{{{a^6}{k^2}}}{x_0^2}-{a^2}{b^2}=0$,
判别式$△=({a^4}-{a^2}x_0^2){k^2}-{b^2}x_0^2$,…(1),
因为点G在椭圆C上,所以$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$,…(2)
又$k=\frac{y_0}{{{x_0}-\frac{a^2}{x_0}}}=\frac{{{x_0}{y_0}}}{{x_0^2-{a^2}}}$,…(3)
把(2)(3)代入(1)得:
判别式$△=({a^4}-{a^2}x_0^2){(\frac{{{x_0}{y_0}}}{{x_0^2-{a^2}}})^2}-{b^2}x_0^2=\frac{{x_0^2({a^2}y_0^2+{b^2}x_0^2-{a^2}{b^2})}}{{{a^2}-x_0^2}}=0$,
所以直线GN为所求的切线.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率公式和方程的运用,注意直线方程和椭圆方程联立,运用判别式为0,考查化简整理的运算求解能力,属于中档题.

| A. | 2+i | B. | 2-i | C. | -1-2i | D. | -1+i |
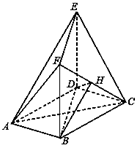 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.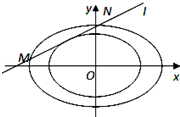 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{1}{2}$,点M在椭圆C上,点M到椭圆C的两个焦点的距离之和是4.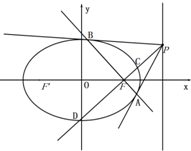 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.