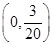题目内容
.(本题14分)过点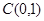 的椭圆
的椭圆 (
(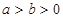 )的离心率为
)的离心率为 ,椭圆与
,椭圆与 轴的交于两点
轴的交于两点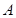 (
(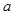 ,
,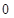 ),
),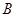 (
( ,
,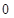 ),过点
),过点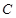 的直线
的直线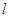 与椭圆交于另一点
与椭圆交于另一点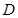 ,并与
,并与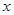 轴交于点
轴交于点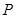 ,直线
,直线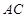 与直线
与直线 叫与点
叫与点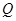 .
.
(I)当直线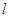 过椭圆右交点时,求线段
过椭圆右交点时,求线段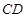 的长;
的长;
(II)当点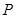 异于
异于 两点时,求证:
两点时,求证: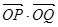 为定值.
为定值.
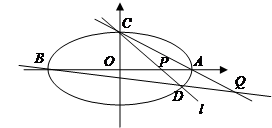
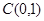 的椭圆
的椭圆 (
(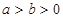 )的离心率为
)的离心率为 ,椭圆与
,椭圆与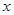 轴的交于两点
轴的交于两点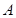 (
(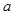 ,
,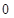 ),
),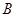 (
( ,
,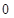 ),过点
),过点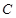 的直线
的直线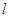 与椭圆交于另一点
与椭圆交于另一点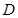 ,并与
,并与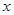 轴交于点
轴交于点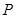 ,直线
,直线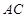 与直线
与直线 叫与点
叫与点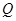 .
.(I)当直线
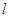 过椭圆右交点时,求线段
过椭圆右交点时,求线段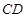 的长;
的长;(II)当点
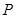 异于
异于 两点时,求证:
两点时,求证: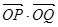 为定值.
为定值.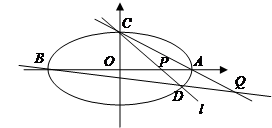
解:(I)由已知得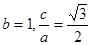 ,解得
,解得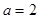
∴ 椭圆方程为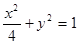 ,--------------------3分
,--------------------3分
右焦点为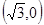 ,直线
,直线 的方程为
的方程为  ,
,
代入椭圆方程化简得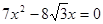 ,∴
,∴ 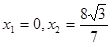 , -------4分
, -------4分
代入直线 的方程得
的方程得 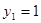 ,
,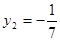 ,所以,D点坐标为
,所以,D点坐标为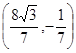 .-------5分
.-------5分
故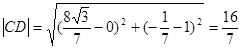 -------------------7分
-------------------7分
(II))当直线 与
与 轴垂直时与题意不符, -------------------8分
轴垂直时与题意不符, -------------------8分
当直线 与
与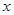 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 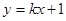 (
(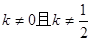 )-------9分
)-------9分
代入椭圆方程化简得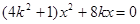 ,
,
解得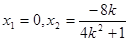 ,
,
代入直线 的方程得
的方程得 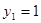 ,
,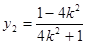
所以,D点坐标为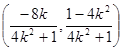 -------------------11分
-------------------11分
又直线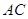 的方程为
的方程为  ,直线
,直线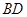 的方程为
的方程为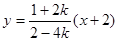
联立解得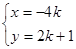 , -----------------------------13分
, -----------------------------13分
因此点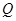 的坐标为(
的坐标为(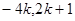 ),又
),又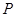 点坐标为(
点坐标为(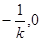 ),
),
所以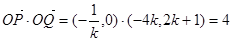
故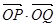 为定值. -----------------------------14分
为定值. -----------------------------14分
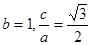 ,解得
,解得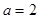
∴ 椭圆方程为
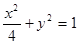 ,--------------------3分
,--------------------3分右焦点为
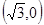 ,直线
,直线 的方程为
的方程为  ,
,代入椭圆方程化简得
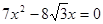 ,∴
,∴ 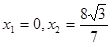 , -------4分
, -------4分代入直线
 的方程得
的方程得 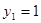 ,
,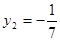 ,所以,D点坐标为
,所以,D点坐标为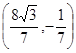 .-------5分
.-------5分故
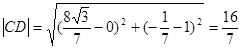 -------------------7分
-------------------7分(II))当直线
 与
与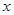 轴垂直时与题意不符, -------------------8分
轴垂直时与题意不符, -------------------8分当直线
 与
与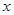 轴不垂直时,设直线
轴不垂直时,设直线 的方程为
的方程为 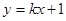 (
(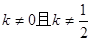 )-------9分
)-------9分代入椭圆方程化简得
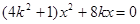 ,
,解得
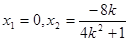 ,
, 代入直线
 的方程得
的方程得 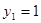 ,
,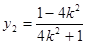
所以,D点坐标为
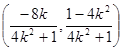 -------------------11分
-------------------11分又直线
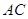 的方程为
的方程为  ,直线
,直线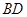 的方程为
的方程为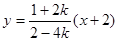
联立解得
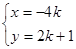 , -----------------------------13分
, -----------------------------13分因此点
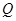 的坐标为(
的坐标为(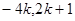 ),又
),又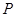 点坐标为(
点坐标为(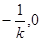 ),
),所以
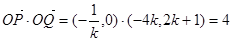
故
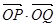 为定值. -----------------------------14分
为定值. -----------------------------14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的长轴
的长轴 分成
分成 等份,过每个分点作
等份,过每个分点作 轴的垂线交椭圆的上半部分于
轴的垂线交椭圆的上半部分于 七个点,
七个点, 是椭圆的一个焦点,则
是椭圆的一个焦点,则 ( ).
( ).
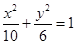 有公共的焦点,则双曲线C的方程为____________。
有公共的焦点,则双曲线C的方程为____________。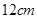 的圆柱被与底面成
的圆柱被与底面成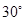 的平面所截,其截口是一个椭圆,则这个椭圆的离心率为 .
的平面所截,其截口是一个椭圆,则这个椭圆的离心率为 .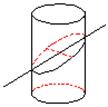
 中,
中, 为椭圆上的一点,过坐标原点
为椭圆上的一点,过坐标原点 的直线交椭圆于
的直线交椭圆于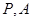 两点,其中
两点,其中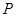 在第一象限,过
在第一象限,过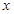 轴的垂线,垂足为
轴的垂线,垂足为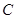 ,连接
,连接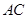 ,
, 与
与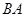 的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;
的斜率均存在,问它们的斜率之积是否为定值,若是,求出这个定值,若不是,说明理由;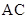 的延长线与椭圆的交点,求证:
的延长线与椭圆的交点,求证: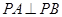 .
.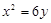 的焦点为F,椭圆C:
的焦点为F,椭圆C: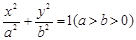 的离心率为
的离心率为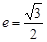 ,
,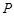 是它们的一个交点,且
是它们的一个交点,且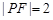 .
. ,点A,B为椭圆
,点A,B为椭圆 上的两点,且弦AB不平行于对称轴,
上的两点,且弦AB不平行于对称轴, 是
是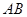 的中点,试探究
的中点,试探究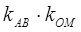 是否为定值,若不是,请说明理由。
是否为定值,若不是,请说明理由。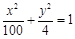 的左焦点F引圆
的左焦点F引圆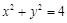 的切线FT交椭圆于点P,切点T位于F、P之间,M为线段FP的中点,M位于F、T之间,则
的切线FT交椭圆于点P,切点T位于F、P之间,M为线段FP的中点,M位于F、T之间,则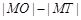 的值为_____________
的值为_____________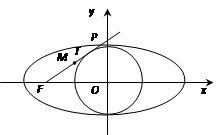
 中有一直角梯形
中有一直角梯形 ,
,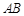 的中点为
的中点为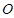 ,
,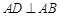 ,
,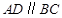 ,
,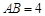 ,
,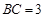 ,
,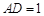 ,以
,以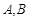 为焦点的椭圆经过点
为焦点的椭圆经过点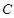 .
.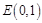 ,问是否存在直线
,问是否存在直线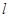 与椭圆交于
与椭圆交于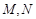 两点且
两点且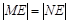 ,若存在,求出直线
,若存在,求出直线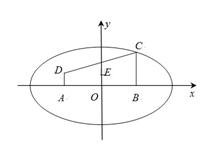
 的焦点坐标为【 】
的焦点坐标为【 】  ,
,
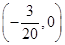 ,
,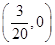
 ,
,