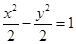题目内容
等轴双曲线C与椭圆
有公共的焦点，则双曲线C的方程为____________。
有公共的焦点，则双曲线C的方程为____________。
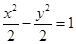
椭圆的焦点坐标为
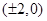，则设等轴双曲线方程为
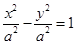，从而有
，解得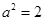
，所以双曲线方程为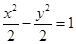
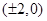的焦点坐标为，则设等轴双曲线方程为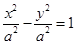，从而有，解得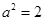，所以双曲线方程为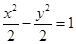
练习册系列答案
相关题目
题目内容
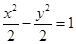
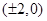有公共的焦点，则双曲线C的方程为____________。的焦点坐标为，则设等轴双曲线方程为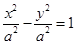，从而有，解得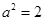，所以双曲线方程为
上任意一点，
为左、右焦点，
如图所示．
的中点为
，求证:
，求|PF1|·|PF2|之值；
的离心率
，右焦点到直线
的距离为
，过
的直线
交椭圆于
两点.(Ⅰ) 求椭圆的方程；（Ⅱ） 若直线
轴于
,
,求直线
的焦点为
、
，点
在椭圆上，若
，则
___．
(
)的左焦点
作
轴的垂线交椭圆于点
，
为右焦点，若
，则椭圆的离心率为( )
的方程为
，称圆心在坐标原点
，半径为
的圆为椭圆
的“伴随圆”，椭圆
．
与椭圆
两点，与其“伴随圆”交于
两点，当
时，求△
面积的最大值．
上的点到右焦点F的最小距离是
，
到上顶点的距离为
，点
是线段
上的一个动点.
轴不垂直的直线
与椭圆交于
、
两点,使得
,并说明理由.
的椭圆
（
）的离心率为
，椭圆与
轴的交于两点
（
，
），
（
，
的直线
与椭圆交于另一点
，并与
，直线
与直线
叫与点
．
的长；
两点时，求证：
为定值．
与双曲线
有共同的焦点，
