题目内容
17.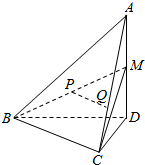 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.(1)证明:BC⊥CM;(2)证明:PQ∥平面BCD.
分析 (1)由AD与平面BCD垂直,得到BC与AD垂直,进而得到BC与平面ACD垂直,即可得证;
(2)取BD的中点E,在线段CD上取点F,使得DF=3FC,连接PE,EF,QF,利用中位线定理得到PE与DM平行,进而得到PE与AD平行,等于AD的四分之一,在三角形CAD中,根据题意得到QF与AD平行,且QF等于AD的四分之一,得到PE与QF平行且相等,进而确定出四边形EFQP为平行四边形,得到PQ与EF平行,即可得证.
解答  证明:(1)∵AD⊥平面BCD,BC?平面BCD,
证明:(1)∵AD⊥平面BCD,BC?平面BCD,
∴BC⊥AD,
又BC⊥CD,且CD、AD?平面ACD,CD∩AD=D,
∴BC⊥平面ACD,
∵CM?平面ACD
∴BC⊥CM;
(2)取BD的中点E,在线段CD上取点F,使得DF=3FC,连接PE,EF,QF,
∵P、E分别是BM、BD的中点,
∴PE为△BDM的中位线,
∴PE∥DM,且PE=$\frac{1}{2}$DM,即PE∥AD,且PE=$\frac{1}{4}$AD,
在△CAD中,AQ=3QC,DF=3FC,
∴QF∥AD,且QF=$\frac{1}{4}$AD,
∴PE∥QF,且PE=QF,
∴四边形EFQP为平行四边形,
∴PQ∥EF,
∵EF?平面BCD,PQ?平面BCD,
∴PQ∥平面BCD.
点评 此题考查了直线与平面垂直的性质,直线与平面平行的判定,熟练掌握性质与判定是解本题的关键.

练习册系列答案
相关题目
7.设S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$+…+$\sqrt{1+\frac{1}{201{4}^{2}}+\frac{1}{201{5}^{2}}}$,则不大于S的最大整数等于( )
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
8.已知数列{an}的通项公式为an=n+$\frac{c}{n}$,若对任意n∈N+,都有an≥a3,则实数c的取值范围是( )
| A. | [6,12] | B. | (6,12) | C. | [5,12] | D. | (5,12) |
5.已知a<b<0,则下列不等式一定成立的是( )
| A. | a2<ab | B. | |a|<|b| | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | ${({\frac{1}{2}})^a}<{({\frac{1}{2}})^b}$ |
7.设随机变量X的概率分布如表所示:
则X的方差为2.
| X | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{1}{5}$ |
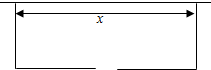 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽2m的进出口,如图所示.已知旧墙的维修费用为45元/m,新墙的造价为180元/m.设利用旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元).