题目内容
7.设S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$+…+$\sqrt{1+\frac{1}{201{4}^{2}}+\frac{1}{201{5}^{2}}}$,则不大于S的最大整数等于( )| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
分析 由$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$,利用裂项求和法求出S=2014+1-$\frac{1}{2015}$,由此能求出不大于S的最大整数为2014.
解答 解:$\sqrt{1+\frac{1}{{n}^{2}}+\frac{1}{(n+1)^{2}}}$=$\frac{\sqrt{{n}^{2}(n+1)^{2}+{n}^{2}+(n+1)^{2}}}{n(n+1)}$=$\frac{\sqrt{(1+n+{n}^{2})^{2}}}{{n}^{2}+n}$=$\frac{1+n+{n}^{2}}{{n}^{2}+n}$=1+$\frac{1}{n}$-$\frac{1}{n+1}$,
∴S=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$+…+$\sqrt{1+\frac{1}{201{4}^{2}}+\frac{1}{201{5}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$+1+$\frac{1}{2}$-$\frac{1}{3}$+1+$\frac{1}{3}$-$\frac{1}{4}$+…+1+$\frac{1}{2014}$-$\frac{1}{2015}$=2014+1-$\frac{1}{2015}$,
∴不大于S的最大整数为2014,
故选:C.
点评 本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
| A. | y=|x| | B. | y=-x3 | C. | y=-(x+1)2 | D. | y=-x2 |
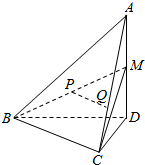 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.