题目内容
2.已知函数$f(x)=a+\frac{1}{{{4^x}-1}}$的图象关于原点对称,则实数a值是$\frac{1}{2}$.分析 根据函数奇偶性和图象的对称关系进行求解即可.
解答 解:∵函数$f(x)=a+\frac{1}{{{4^x}-1}}$的图象关于原点对称,
∴函数f(x)是奇函数,
则f(-x)=-f(x),
即a+$\frac{1}{{4}^{-x}-1}$=-(a+$\frac{1}{{4}^{x}-1}$)=-a-$\frac{1}{{4}^{x}-1}$,
即2a=-$\frac{1}{{4}^{-x}-1}$-$\frac{1}{{4}^{x}-1}$=$-\frac{{4}^{x}}{1-{4}^{x}}$-$\frac{1}{{4}^{x}-1}$=$\frac{{4}^{x}-1}{{4}^{x}-1}$=1,
解得a=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 本题主要考查函数奇偶性的性质的应用,根据奇函数的关系式f(-x)=-f(x)建立方程关系是解决本题的关键.

练习册系列答案
相关题目
13.设Sn为正项等比数列{an}的前n项和,且4a1-a3=0,则$\frac{{S}_{3}}{{a}_{1}}$=( )
| A. | 3 | B. | 7 | C. | $\frac{7}{4}$ | D. | 3或7 |
14.已知命题p:若x>y,则-x<-y;命题q:若x<y,则x2>y2;在下列命题中:(1)p∧q;(2)p∨q;(3)p∧(¬q);(4)(¬p)∨q,真命题是( )
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
11.若某空间几何体的三视图如图所示,则该几何体的体积为( )
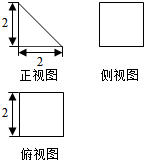

| A. | $\frac{8}{3}$ | B. | 8 | C. | 4 | D. | $\frac{4}{3}$ |
12.已知向量$\overrightarrow{a}$=(4,2),$\overrightarrow{b}$=(x,3),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值为( )
| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.