题目内容
设椭圆M：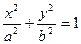
(a＞b＞0)的离心率为
，长轴长为
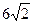，设过右焦点F倾斜角为
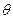的直线交椭圆M于A，B两点。
（Ⅰ）求椭圆M的方程；
（Ⅱ）求证| AB | =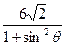
；
（Ⅲ）设过右焦点F且与直线AB垂直的直线交椭圆M于C，D，求|AB| + |CD|的最小值。
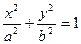(a＞b＞0)的离心率为，长轴长为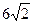，设过右焦点F倾斜角为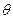的直线交椭圆M于A，B两点。（Ⅰ）求椭圆M的方程；
（Ⅱ）求证| AB | =
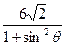；（Ⅲ）设过右焦点F且与直线AB垂直的直线交椭圆M于C，D，求|AB| + |CD|的最小值。
（Ⅰ）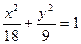
；（Ⅱ）略；（Ⅲ）
。
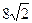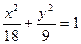；（Ⅱ）略；（Ⅲ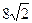）。解：（Ⅰ）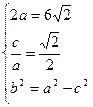
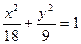所求椭圆M的方程为…4分
（Ⅱ）当≠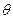
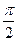，设直线AB的斜率为k = tan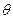，焦点F ( 3 , 0 )，则直线AB的方程为
y = k ( x – 3 ) 有
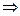( 1 + 2k2 )x2 – 12k2x + 18( k2 – 1 ) =" 0"
设点A ( x1 , y1 ) , B ( x2 , y2 ) 有x1 + x2 =
, x1x2 =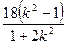
|AB| =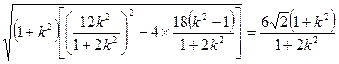
** … 6分
又因为 k = tan=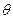
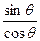代入**式得
|AB| =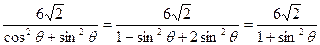
………… 8分
当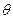=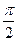时，直线AB的方程为x = 3，此时|AB| =
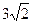……………… 10分
而当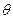=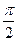时，|AB| ==
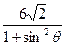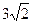
综上所述：所以|AB| =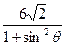……………… 11分
（Ⅲ）过右焦点F且与直线AB垂直的直线交椭圆M于C，D，
同理可得 |CD| =
=
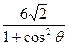……………………… 12分
有|AB| + |CD| =+=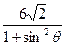
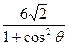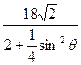
因为sin2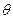∈[0，1]，所以 当且仅当sin2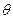=1时，|AB|+|CD|有最小值是 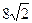…… 16分
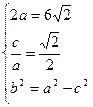
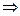
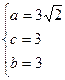所求椭圆M的方程为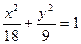…4分（Ⅱ）当
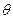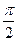≠，设直线AB的斜率为k = tan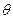，焦点F ( 3 , 0 )，则直线AB的方程为y = k ( x – 3 ) 有
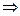( 1 + 2k2 )x2 – 12k2x + 18( k2 – 1 ) =" 0" 设点A ( x1 , y1 ) , B ( x2 , y2 ) 有x1 + x2 =
, x1x2 =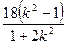|AB| =
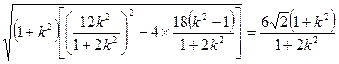** … 6分又因为 k = tan
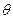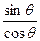= 代入**式得|AB| =
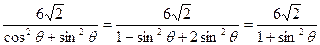………… 8分当
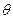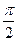=时，直线AB的方程为x = 3，此时|AB| =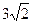……………… 10分而当
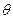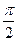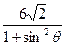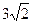
=时，|AB| ==综上所述：所以|AB| =
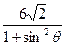……………… 11分（Ⅲ）过右焦点F且与直线AB垂直的直线交椭圆M于C，D，
同理可得 |CD| =
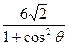= ……………………… 12分有|AB| + |CD| =
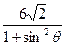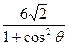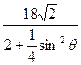
+=因为sin2
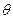∈[0，1]，所以 当且仅当sin2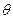=1时，|AB|+|CD|有最小值是 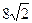…… 16分
练习册系列答案
相关题目
+ 
=1(x≠±2)
+
=1(y≠±2)
，求△AOB面积的最大值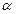
（
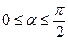）方向行走一段时间后，再向正北方向行走一段时间，但何时改变方向不定。假定机器人行走速度为10米/分钟，则机器人行走2分钟时的可能落点区域的面积是 。
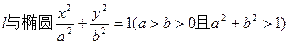相交于P、Q两点，PQ中点坐标为
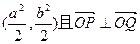（O为坐标原点）。（I）求直线
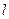的方程；（II）证明：
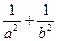为定值。
)
)
满足
,求
的最大值与最小值