题目内容
设F1、F2是双曲线x2-y2=4的左、右两个焦点,P是双曲线上任意一点,过F1作∠F1PF2的平分线的垂线,垂足为M,求点M的轨迹方程.
x2+y2=4.
如图,F1(-2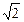 ,0)、F2(2
,0)、F2(2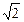 ,0)、M(x,y),
,0)、M(x,y),
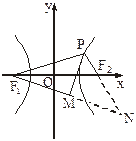
延长F1M与PF2相交于点N,设N(x0,y0).
由已知可得M为F1N的中点,
∴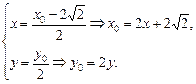
又|NF2|=|PN|-|PF2|=|PF1|-|PF2|=2a=4,
∴(x0-2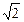 )2+y02=16.
)2+y02=16.
∴(2x+2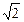 -2
-2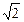 )2+(2y)2=16.∴x2+y2=4.
)2+(2y)2=16.∴x2+y2=4.
评注:适当运用平面几何知识把条件进行转化,会给我们解题带来方便.
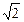 ,0)、F2(2
,0)、F2(2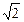 ,0)、M(x,y),
,0)、M(x,y),
延长F1M与PF2相交于点N,设N(x0,y0).
由已知可得M为F1N的中点,
∴
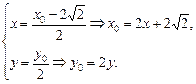
又|NF2|=|PN|-|PF2|=|PF1|-|PF2|=2a=4,
∴(x0-2
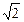 )2+y02=16.
)2+y02=16.∴(2x+2
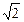 -2
-2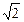 )2+(2y)2=16.∴x2+y2=4.
)2+(2y)2=16.∴x2+y2=4.评注:适当运用平面几何知识把条件进行转化,会给我们解题带来方便.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
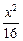 +
+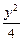 =1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.
=1,过点P(2,1)引一条弦,使它在这点被平分,求此弦所在的直线方程.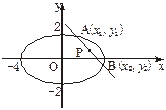
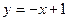 与椭圆
与椭圆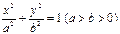 相交于A、B两点.。
相交于A、B两点.。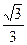 ,焦距为2,求线段AB的长;
,焦距为2,求线段AB的长;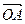 与向量
与向量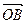 互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.
互相垂直(其中O为坐标原点),当椭圆的离心率e=2时,求椭圆的长轴的长.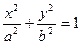 (a>b>0)的离心率为
(a>b>0)的离心率为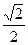 ,长轴长为
,长轴长为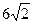 ,设过右焦点F倾斜角为
,设过右焦点F倾斜角为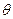 的直线交椭圆M于A,B两点。
的直线交椭圆M于A,B两点。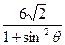 ;
;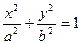 上有一点M(-4,
上有一点M(-4,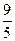 )在抛物线
)在抛物线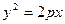 (p>0)的准线l上,抛物线的焦点也是椭圆焦点.
(p>0)的准线l上,抛物线的焦点也是椭圆焦点.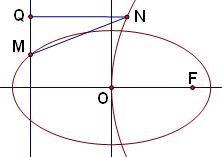
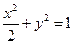 的右准线
的右准线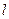 与
与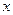 轴相交于点
轴相交于点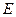 ,过椭圆右焦点
,过椭圆右焦点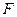 的直线与椭圆相交于
的直线与椭圆相交于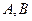 两点,点
两点,点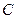 在右准线上,且
在右准线上,且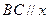 轴。
轴。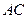 经过线段
经过线段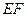 的中点。
的中点。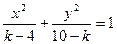 表示焦点在
表示焦点在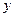 轴上的椭圆,则实数
轴上的椭圆,则实数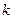 的取值范围是____________
的取值范围是____________