题目内容
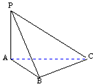
如图,四棱锥P-ABCD的底面为菱形且∠DAB=60°,PA⊥底面ABCD,AB=2,PA=2
,E为PC的中点.
(1)求直线DE与平面PAC所成角的大小;
(2)求C点到平面PBD的距离.

| 3 |
(1)求直线DE与平面PAC所成角的大小;
(2)求C点到平面PBD的距离.

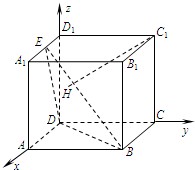
(1)如图,连AC,BD交于点O,又由底面ABCD为菱形可得BD⊥AC,且点O是AC的中点,连接OE,又E为PC的中点,所以EO∥PA.
由PA⊥底面ABCD,可得EO⊥底面ABCD
以O为原点,OA,OB,OE分别为x,y,z轴建立空间直角坐标系
则有O(0,0,0),A(
,0,0),B(0,1,0),C(-
,0,0),D(0,-1,0),P(
,0,2
),E(0,0,
)
依题意得
=(0,2,0)即为平面PAC的一个法向量
又
=(0,1,
),所以cos<
,
>=
=
所以<
,
>=60°直线DE与平面PAC所成角的大小为30°
(2)由(1)知,
=(0,2,0),
=(
,1,2
),
=(
,-1,0)
设
=(x,y,z)为平面PBD的一个法向量
由
⊥
与
⊥
得
令x=1,取
=(1,0,-2)∴C点到平面PBD的距离为d,
则d=
=
=
.

由PA⊥底面ABCD,可得EO⊥底面ABCD
以O为原点,OA,OB,OE分别为x,y,z轴建立空间直角坐标系
则有O(0,0,0),A(
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
依题意得
| DB |
又
| DE |
| 3 |
| DB |
| DE |
| 2 |
| 2×2 |
| 1 |
| 2 |
所以<
| DB |
| DE |
(2)由(1)知,
| DB |
| DP |
| 3 |
| 3 |
| CD |
| 3 |
设
| n |
由
| n |
| DB |
| n |
| DP |
|
令x=1,取
| n |
则d=
|
| ||||
|
|
| ||
|
3
| ||
| 5 |


练习册系列答案
相关题目