题目内容
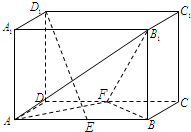
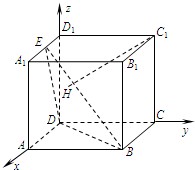
[理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,
={2m,-2m,-m}(m<0)
(1)证明HC1⊥平面EDB;
(2)求BC1与平面EDB所成的角;
(3)若正方体的棱长为a,求三棱锥A-EDB的体积.
[文]若数列{an}的通项公式an=
(n∈N+),记f(n)=(1-a1)(1-a2)…(1-an).
(1)计算f(1),f(2),f(3)的值;
(2)由(1)推测f(n)的表达式;
(3)证明(2)中你的结论.
| HC1 |
(1)证明HC1⊥平面EDB;
(2)求BC1与平面EDB所成的角;
(3)若正方体的棱长为a,求三棱锥A-EDB的体积.
[文]若数列{an}的通项公式an=
| 1 |
| (n+1)2 |
(1)计算f(1),f(2),f(3)的值;
(2)由(1)推测f(n)的表达式;
(3)证明(2)中你的结论.

[理](1)设正方体的棱长为a,
则
={
,0,a},
={a,a,0},
∵
•
=0,
•
=0,
∴
⊥
,
⊥
,又DE∩DB=D,
∴HC1⊥平面EDB.
(2)
={-a,0,a},
设
与
所成的角为θ,
cosθ=
=
=
∴θ=45°.
由(1)知HC1⊥平面EDB,
∴∠C1BH为BC1与平面EDB所成的角.
∠C1BH=90°-45°=45°.
(3)VA-EDB=VE-ABD=
•
a2•a=
a3
[文](1)a1=
,a2=
,a3=
,a4=
,f(1)=1-a1=
f(2)=(1-a1)(1-a2)=
,
f(3)=(1-a1)(1-a2)(1-a3)=
,f(4)=(1-a1)(1-a2)(1-a3)(1-a4)=
,
(2)故猜想f(n)=
(n∈N*)
(3)证明:1-an=1-
=
=
•
1-an-1=
•
1-an-2=
•
1-an-3=
•
…1-a3=
•
1-a2=
•
1-a1=
•
将上述n个因式相乘得:(1-a1)(1-a2)(1-an)=
•
=
即f(n)=
(n∈N*)
则
| DE |
| a |
| 2 |
| DB |
∵
| HC1 |
| DE |
| HC1 |
| DB |
∴
| HC1 |
| DE |
| HC1 |
| DB |
∴HC1⊥平面EDB.
(2)
| BC1 |
设
| BC1 |
| HC1 |
cosθ=
| ||||
|
|
| 2ma+ma | ||
|
| ||
| 2 |
∴θ=45°.
由(1)知HC1⊥平面EDB,
∴∠C1BH为BC1与平面EDB所成的角.
∠C1BH=90°-45°=45°.
(3)VA-EDB=VE-ABD=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
[文](1)a1=
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| 25 |
| 3 |
| 4 |
| 2 |
| 3 |
f(3)=(1-a1)(1-a2)(1-a3)=
| 5 |
| 8 |
| 3 |
| 5 |
(2)故猜想f(n)=
| n+2 |
| 2(n+1) |
(3)证明:1-an=1-
| 1 |
| (n+1)2 |
| n2+2n |
| (n+1)2 |
| n+2 |
| n+1 |
| n |
| n+1 |
1-an-1=
| n+1 |
| n |
| n-1 |
| n |
1-an-2=
| n |
| n-1 |
| n-2 |
| n-1 |
1-an-3=
| n-1 |
| n-2 |
| n-3 |
| n-2 |
| 5 |
| 4 |
| 3 |
| 4 |
1-a2=
| 4 |
| 3 |
| 2 |
| 3 |
1-a1=
| 3 |
| 2 |
| 1 |
| 2 |
将上述n个因式相乘得:(1-a1)(1-a2)(1-an)=
| n+2 |
| n+1 |
| 1 |
| 2 |
| n+2 |
| 2(n+1) |
即f(n)=
| n+2 |
| 2(n+1) |

练习册系列答案
相关题目