题目内容
如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC.
(1)求证:AM⊥平面EBC;
(2)求二面角A-EB-C的大小.

(1)求证:AM⊥平面EBC;
(2)求二面角A-EB-C的大小.

∵四边形ACDE是正方形,所以EA⊥AC,AM⊥EC,
∵平面ACDE⊥平ABC,
∴EA⊥平面ABC,
∴可以以点A为原点,以过A点平行于BC的直线为x轴,
分别以直线AC和AE为y轴和z轴,建立如图所示的空间直角坐标系A-xyz.
设EA=AC=BC=2,则A(0,0,0),B(2,2,0),C(0,2,0),E(0,0,2),
∵M是正方形ACDE的对角线的交点,
∴M(0,1,1).
(1)
=(0,1,1),
=(0,2,0)-(0,0,2)=(0,2,-2),
=(2,2,0)-(0,2,0)=(2,0,0),
∴
•
=0,
•
=0
∴AM⊥EC,AM⊥CB,
∴AM⊥平面EBC.
(2)设平面EBC的法向量为
=(x,y,z),则
⊥
且
⊥
,
∴
•
=0,
•
=0.
∴
,取y=-1,则x=1,则
=(1,-1,0).
又∵
为平面EBC的一个法向量,且)
=(0,1,1),
∴cos<
,
>=
=-
,
设二面角A-EB-C的平面角为θ,则cosθ=|cos<
,
>|=
,
∴二面角A-EB-C等60°.
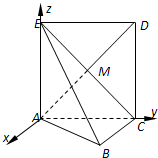
∵平面ACDE⊥平ABC,
∴EA⊥平面ABC,
∴可以以点A为原点,以过A点平行于BC的直线为x轴,
分别以直线AC和AE为y轴和z轴,建立如图所示的空间直角坐标系A-xyz.
设EA=AC=BC=2,则A(0,0,0),B(2,2,0),C(0,2,0),E(0,0,2),
∵M是正方形ACDE的对角线的交点,
∴M(0,1,1).
(1)
| AM |
| EC |
| CB |
∴
| AM |
| EC |
| AM |
| CB |
∴AM⊥EC,AM⊥CB,
∴AM⊥平面EBC.
(2)设平面EBC的法向量为
| n |
| n |
| AE |
| n |
| AB |
∴
| n |
| AE |
| n |
| AB |
∴
|
| n |
又∵
| AM |
| AM |
∴cos<
| n |
| AM |
| ||||
|
|
| 1 |
| 2 |
设二面角A-EB-C的平面角为θ,则cosθ=|cos<
| n |
| AM |
| 1 |
| 2 |
∴二面角A-EB-C等60°.


练习册系列答案
相关题目
 的最小值为 .
的最小值为 .


 =m
=m ,
, =n
=n ,则m+n的值为________.
,则m+n的值为________.
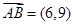 ,则点B的坐标为.
,则点B的坐标为.